What is the ml quantum number for an electron in the 5d orbital?
1 Answer
Explanation:
As you know, the position and spin of an electron in an atom are determined by a set of four quantum numbers
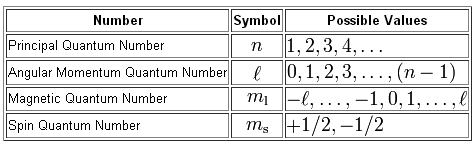
In your case, you're interested about figuring out what value of the magnetic quantum number,
The magnetic quantum number gives you the exact orbital in which the electron is located. The subshell that holds that orbital is determined by the angular momentum quantum number,
As you can see, the values of
#l=0 -># characterizes the s-subshell#l=1 -># characterizes the p-subshell#l=2 -># characterizes the d-subshell
In your case,
#m_l = {-2, -1, color(white)(-)0, color(white)(-)1, color(white)(-)2}#
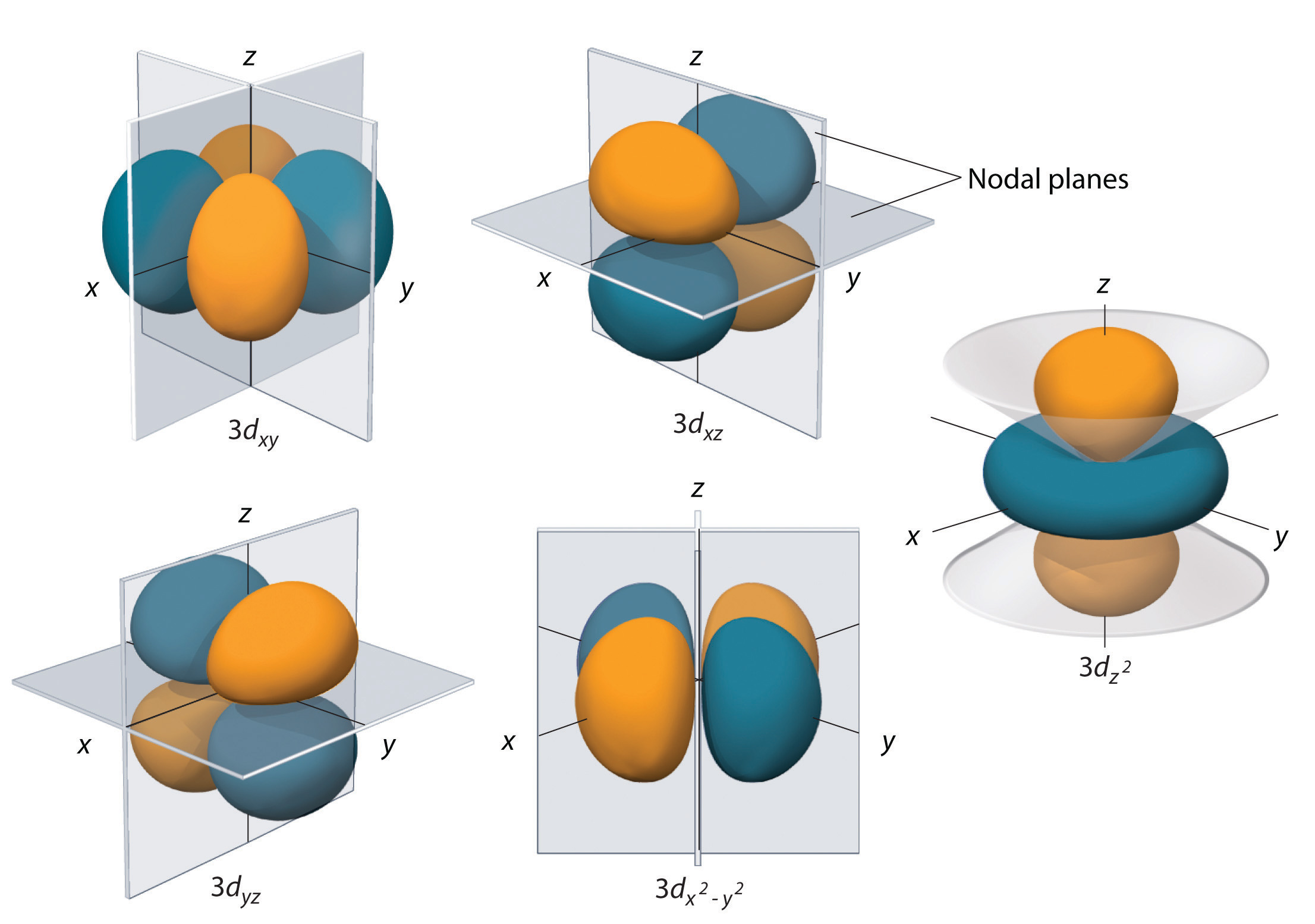
Each d-subshell contains a total of five orbitals. In the case of a 5d-subshell, these orbitals correspond to the following
#m_l = -2 -># the#5d_(xy)# orbital#m_l = -1 -># the#5d_(xz)# orbital#m_l = color(white)(-)0 -># the#5d_(yz)# orbital#m_l = color(white)(-)1 -># the#5d_(x^2-y^2)# orbital#m_l = color(white)(-)2 -># the#5d_(z^2)# orbital