First we need to calculate the oxidation state of #S# atom the usual way.
#S_4O_6^"2-"# : overall oxidation state is -2
[oxidation state of #S# x 4] + [oxidation state of #O# atom x 6] = -2
The most common oxidation state of oxygen is -2. Thus,
[oxidation state of #S# x 4] + [(-2) (6)] = -2
Let #color (red) y# be the oxidation state of #S#. Therefore, we can rewrite the equation as
[(#color (red) y# ) (4)] + [(-2) (6)] = -2
[(#color (red) y# ) (4)] + (-12) = -2
[(#color (red) y# ) (4)] = -2 + (+12)
[(#color (red) y# ) (4)] = +10
#color (red) y# = #(+10)/4#
#color (red) y# = + 2.5
Why the decimal place? Because the individual partial charges of the four #S# atoms are not equal to each other. You need to consider the Lewis structure of this ion.
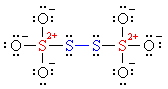
[Notice how the formal charges are given as #+2# on the central sulfurs (#color(red)(red)#) and #0# on the bridging sulfurs (#color(blue)(blue)#). These are not oxidation states!]
The oxidation state +2.5 is just the average oxidation state for the #S# atom.
According to the structure, the symmetry suggests a #-1# on each bridging sulfur (#color(blue)(blue)#) (just like the bridging #O# atoms in a peroxide), and a #+6# (#color(red)(red)#) on each central sulfur (like in sulfate).
Indeed, #(+6 - 1)/2 = 2.5#. Hence, the fractional oxidation state.



