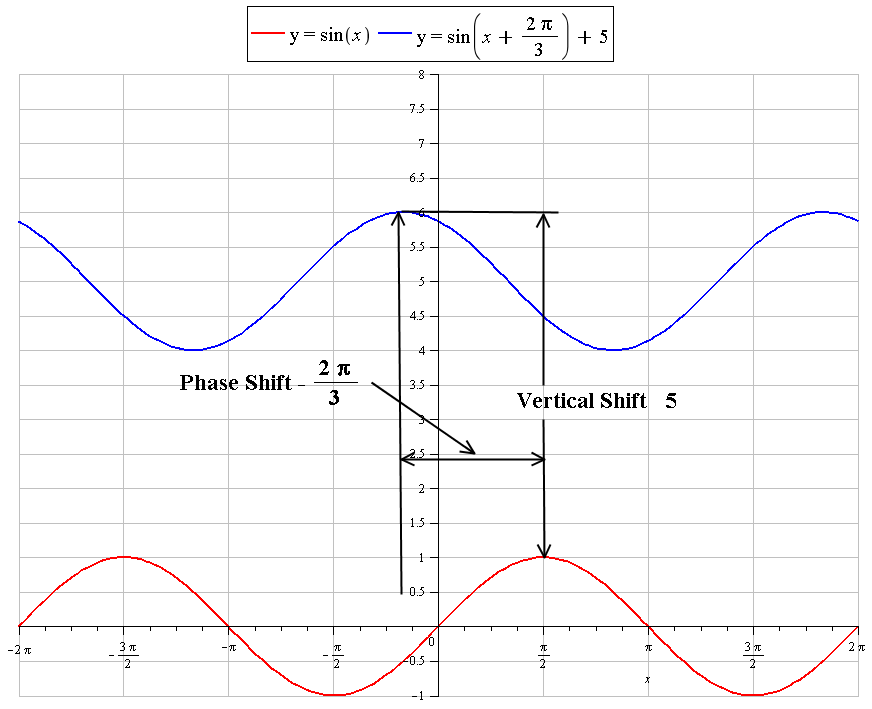
What is the phase shift, vertical displacement with respect to #y=sinx# for the graph #y=sin(x+(2pi)/3)+5#?
1 Answer
See below.
Explanation:
We can represent a trigonometrical function in the following form:
Where:
-
#color(white)(8)bbacolor(white)(88)= "amplitude"# -
#bb((2pi)/b)color(white)(8)= "the period"# ( note#bb(2pi)# is the normal period of the sine function ) -
#bb((-c)/b)color(white)(8)= "the phase shift"# -
#color(white)(8)bbdcolor(white)(888)=" the vertical shift"#
From example:
Amplitude =
Period =
Phase shift =
Vertical shift =
So
Translated 5 units in the positive y direction, and shifted
GRAPH: