What is the polar form of #( -11,121 )#?

1 Answer
Alan P.
Dec 22, 2016

#(r,theta)~~(121.50,1.66)#

Explanation:

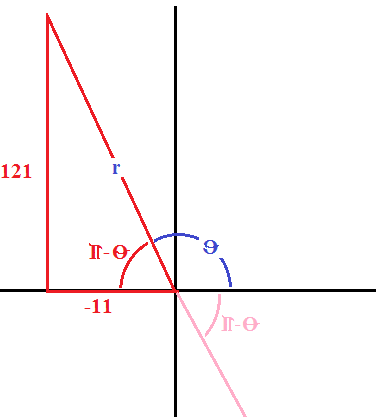
enter image source here

The radius can be calculated using the Pythagorean Theorem as
#color(white)("XXX")color(blue)(r)=sqrt((color(red)(-11))^2+color(red)(121)^2)~~121.4989712#

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

#tan(color(blue)(pi)) = 121/(-11)=-11#

The standard #"arctan"# function gives us the reference angle in either Quadrant I or Quadrant IV (in Q IV in this case since the value of the "tan" is negative).

#arctan(-11)~~-1.48013644# (radians)

#theta = pi + arctan(-11) ~~ 1.661456214#

Related questions
See all questions in Introduction to Polar Coordinates
Impact of this question
1175 views around the world
You can reuse this answer
Creative Commons License