Question

What is the polar form of `( -11,24 )`?

Answer 1

Cartesian form: `(-11,24) <=>` polar form: `(sqrt(597),pi+arctan(-24/11))`

Explanation:

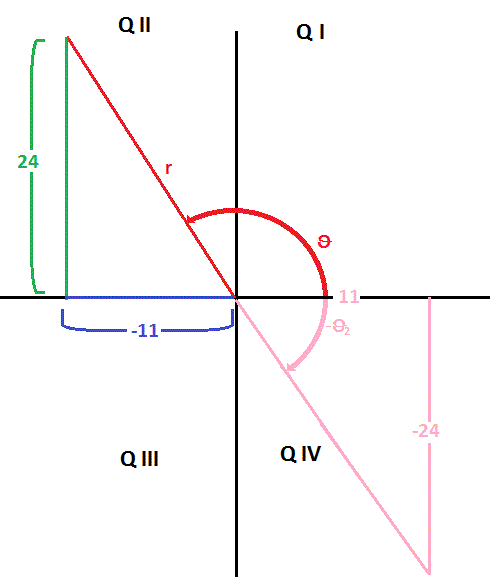
The radius is given by the Pythagorean Theorem as
`color(white)("XXX") r = sqrt((-11)^2+24^2)=sqrt(597)`

`tan(theta) = 24/(-11)`

Unfortunately, `arctan`, the inverse of `tan(theta)` is by definition an angle `in (-pi/2,+pi/2)` (i.e. in QI or Q IV)
[In the diagram above, the angle returned by `arctan(-24/11)` is shown as `theta_2`.]

Taking `arctan(24/(-11)) = arctan((-24)/11)`
gives us an angle that is "pi" radians less than the true value of `theta`

Therefore `theta = pi+arctan(-24/11)`

`(r,theta) = (sqrt(597),pi+arctan(-24/11))`

(using a calculator)
`color(white)("XXX")~~(24.4, 2.0)~~(24.4, 114.6^@)`