What is the polar form of #( -18,-61 )#?
1 Answer
Explanation:
We must first use our knowledge of polar coordinates...
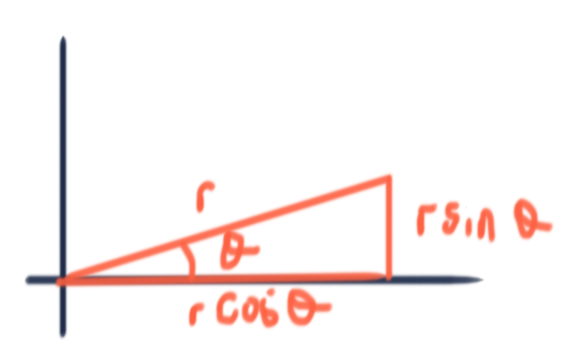
We see from this diagram, that:
So we can find
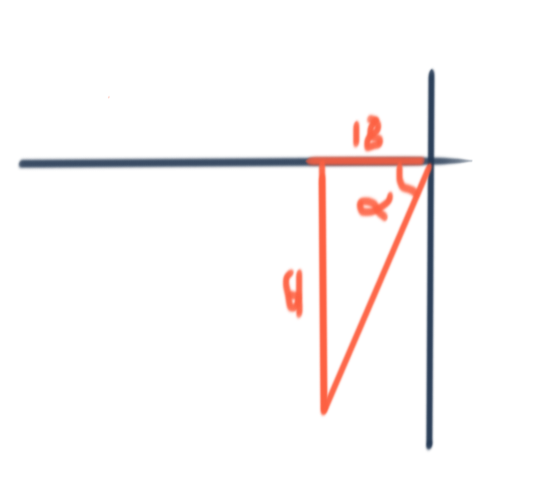
We can now find
Now we need the angle form the positive
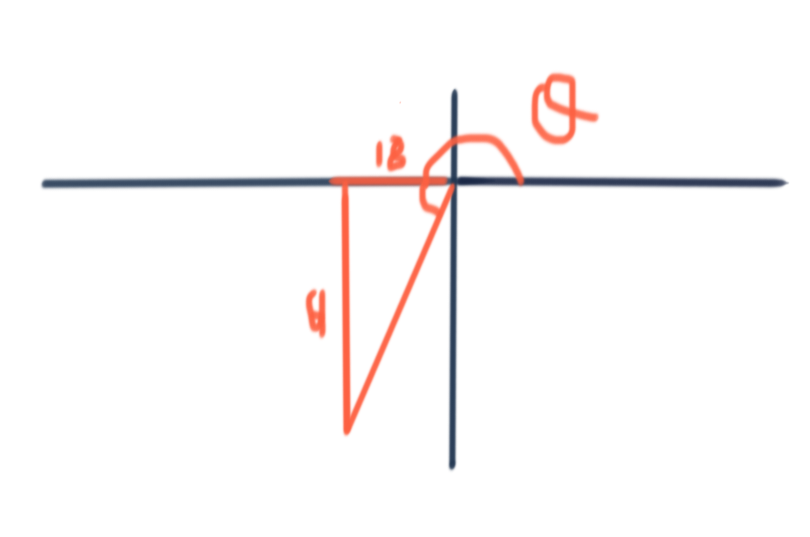
So hence
or
We must first use our knowledge of polar coordinates...

We see from this diagram, that:
So we can find

We can now find
Now we need the angle form the positive

So hence
or