What is the pressure (atm) of 3.5 moles of helium at -50 °C in a rigid container whose volume is 25.0 L?
1 Answer
Jun 25, 2016
Helium has a pressure of 2.56 atm.
Explanation:
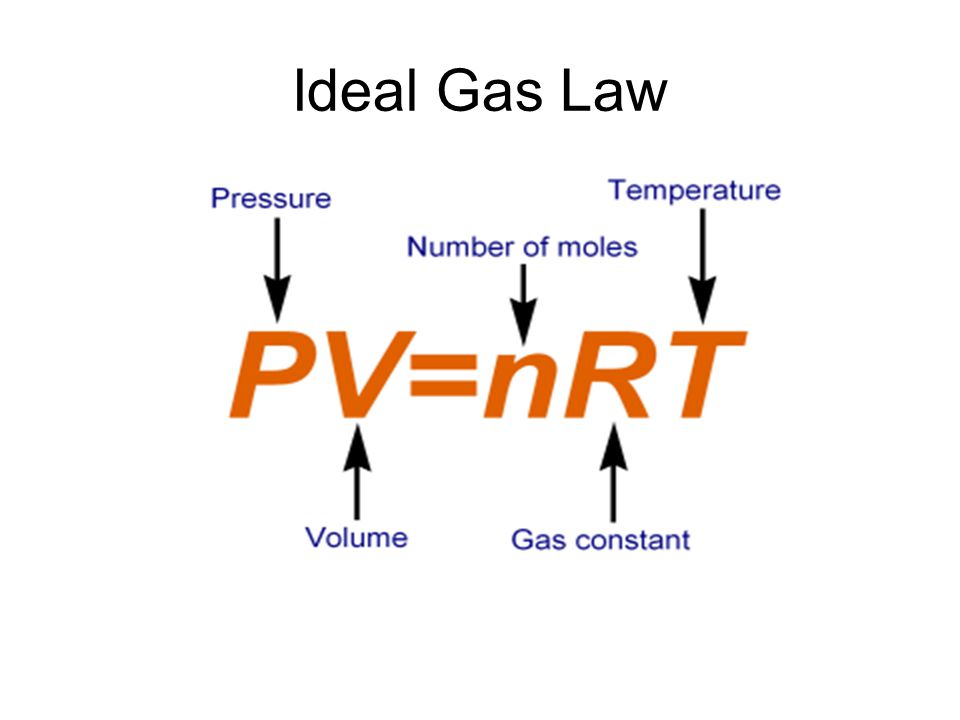
Since we are given the number of moles, temperature, and volume of helium, we have to use the ideal gas law equation to determine the pressure.
 slideplayer.com
slideplayer.com
- P can have units of atm, depending on the units of the universal gas constant
- V must have units of liters
- n should have units of moles
- R has a value of 0.0821 with units of
(Lxxatm)/ (molxxK) - T has units of Kelvins.
Next, list your known and unknown variables. Our only unknown is the pressure of helium. Our known variables are n,V,R, and T.
The only issue is that we have to convert the temperature from centigrade to Kelvins. We can do that using the following conversion:
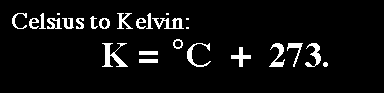 ww2010.atmos.uiuc.edu
ww2010.atmos.uiuc.edu
Therefore,
Now we can rearrange the ideal gas law to solve for P:

