What is the projection of #<< 3, -6, 2 >># onto #<< 3, 2, 1 >>#?

2 Answers
Burglar · Truong-Son N.
May 31, 2016

It is <-3/14, -1/7, -1/14>.

Explanation:

The length of the projection of a vector #v_1# on the vector #v_2# is given by the dot product of #v_1*v_2#.
The dot product is the sum of the products of the components:

#v_1=<3, -6, 2>#
#v_2=<3,2,1>#

#v_1*v_2=3*3+(-6)*2+2*1=9-12+2=-1#.

The direction of the vector is the one of #v_2# but we need to take the unitary vector in that direction that is the vector #v_2# divided by its length.
The length is calculated again with the scalar product, this time of #v_2# by itself (it is like to project the vector on itself)

#||v_2||^2=v_2*v_2=3*3+2*2+1*1=14#

So the unitary vector in the direction of #v_2# is

#\hat{v}_2=v_2/14=<3/14, 2/14, 1/14>=<3/14, 1/7, 1/14>#

This unitary vector gives the direction, while the length and direction was given by the initial dot product that was #-1#.
So the final projection is

#-1*\hat{v}_2=<-3/14, -1/7, -1/14>#.

Truong-Son N.
May 31, 2016

I got #<< -3/14,-1/7,-1/14 >>#, and Wolfram Alpha confirms it.

PROJECTION OF #\mathbf(veca)# ONTO #\mathbf(vecb)#

Let #veca = << 3,-6,2 >># and #vecb = << 3,2,1 >>#.

The projection of #veca# onto #vecb#, which yields a vector, is:

#\mathbf("proj"_(vecb) veca = (vecacdotvecb)/(||vecb||cdot||vecb||)vecb)#

This is drawn as:

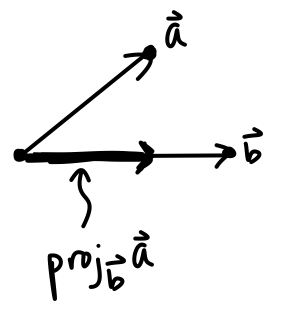
For this, we should define a few more things.

  • The dot product of two #n#-long vectors #vecu# and #vecv#:

#\mathbf(vecucdotvecv)#

#= << u_1,u_2, . . . ,u_N >> cdot << v_1,v_2, . . . ,v_N >>#

#= \mathbf(u_1v_1 + u_2v_2 + . . . + u_Nv_n)#

  • The norm of #vecv#:

#\mathbf(||vecv||)#

#= sqrt(vecvcdotvecv)#

#= sqrt(v_1v_1 + v_2v_2 + . . . + v_Nv_N)#

#= \mathbf(sqrt(v_1^2 + v_2^2 + . . . + v_N^2))#

COMPONENTS OF THE PROJECTION

So, what we now have to do is:

#color(green)(vecacdotvecb)#

#= << 3,-6,2 >>cdot<< 3,2,1 >>#

#= 3*3 + (-6*2) + 2*1#

#= 9 - 12 + 2#

#= color(green)(-1)#

#color(green)(||vecb||)#

#= sqrt(<< 3,2,1 >>cdot << 3,2,1 >>)#

#= sqrt(3*3 + 2*2 + 1*1)#

#= sqrt(9 + 4 + 1)#

#= color(green)(sqrt14)#

FINAL CALCULATION

Finally, put it all back in the first equation.

#color(blue)("proj"_(vecb) veca) = (vecacdotvecb)/(||vecb||cdot||vecb||)vecb#

#= (-1)/(sqrt14*sqrt14)<< 3,2,1 >>#

#= color(blue)(<< -3/14,-1/7,-1/14 >>)#

Related questions
See all questions in Vector Operations
Impact of this question
2733 views around the world
You can reuse this answer
Creative Commons License