What is the range of a function like #f(x)=5x^2#?
1 Answer
Jul 23, 2014
The range of
The range of a function is the set of all possible outputs of that function.
To find the range of this function, we can either graph it, or we can plug in some numbers for
Let's plug in numbers first:
If
If
If
If
If
The lowest number is 0. Therefore the y value for this function can be any number greater than 0.
We can see this more clearly if we graph the function:
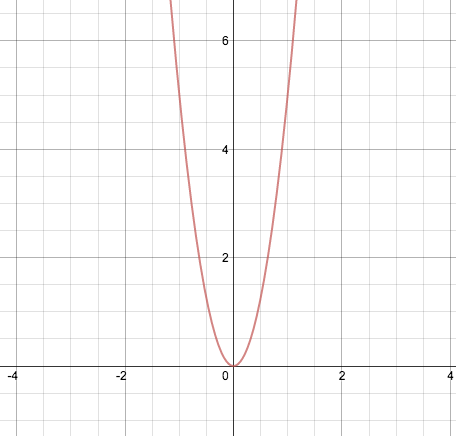
The lowest value of y is 0, therefore the range is all real numbers

