Question

What is the Rover's landing speed? (Picture)

Answer 1

`4.65 ms^-1`

Explanation:

Total energy remains the same during this motion,as motion is only due to the effect of gravity.

So,total energy on top of crater was `m(g/3)h +1/2 mv^2=m(g/3)*1.95+1/2 m 3^2`(Potential energy +Kinetic energy)

While landing it will have purely kinetic energy,so at that time if velocity is `v` then,total energy =`1/2 mv^2`

So,`(1.95mg)/3 +9/2 m=1/2 mv^2`

Solving we get, `v=4.65 ms^-1`

ALTERNATIVELY

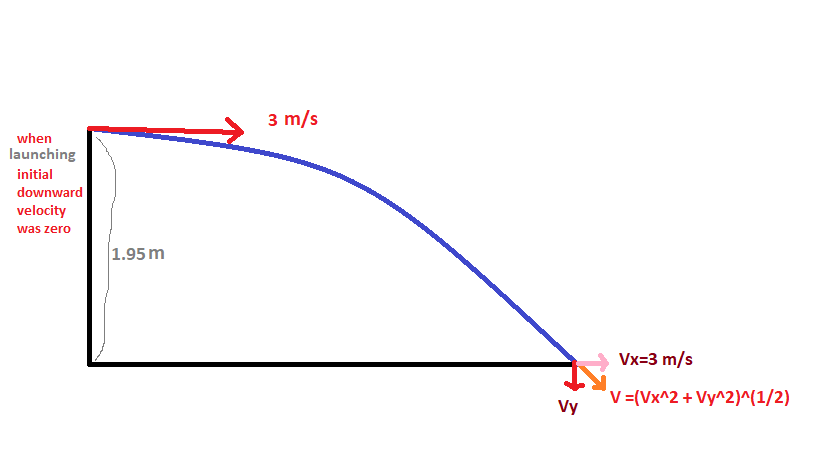
The Mars rover will follow a parabolic path in its journey from the `1.95m` tall crater to the region infront of the bottom of the crater.

Suppose,while landing it will have vertical component of velocity `v_y`,so considering vertical motion only we can write, `v_y^2 =0^2 +2(g/3)*1.95` using `v^2=u^2+2as` the rover was launched with an initial velocity horizontally,so initially it had no vertical component of velocity and `a=g/3`

So,`v_y^2=12.74`

Now,horizontal component of velocity remains the same i.e `v_x=3 m/s`

So,landing velocity = `sqrt(v_x^2 +v_y^2)=3^2 +12.74=4.65ms^-1`