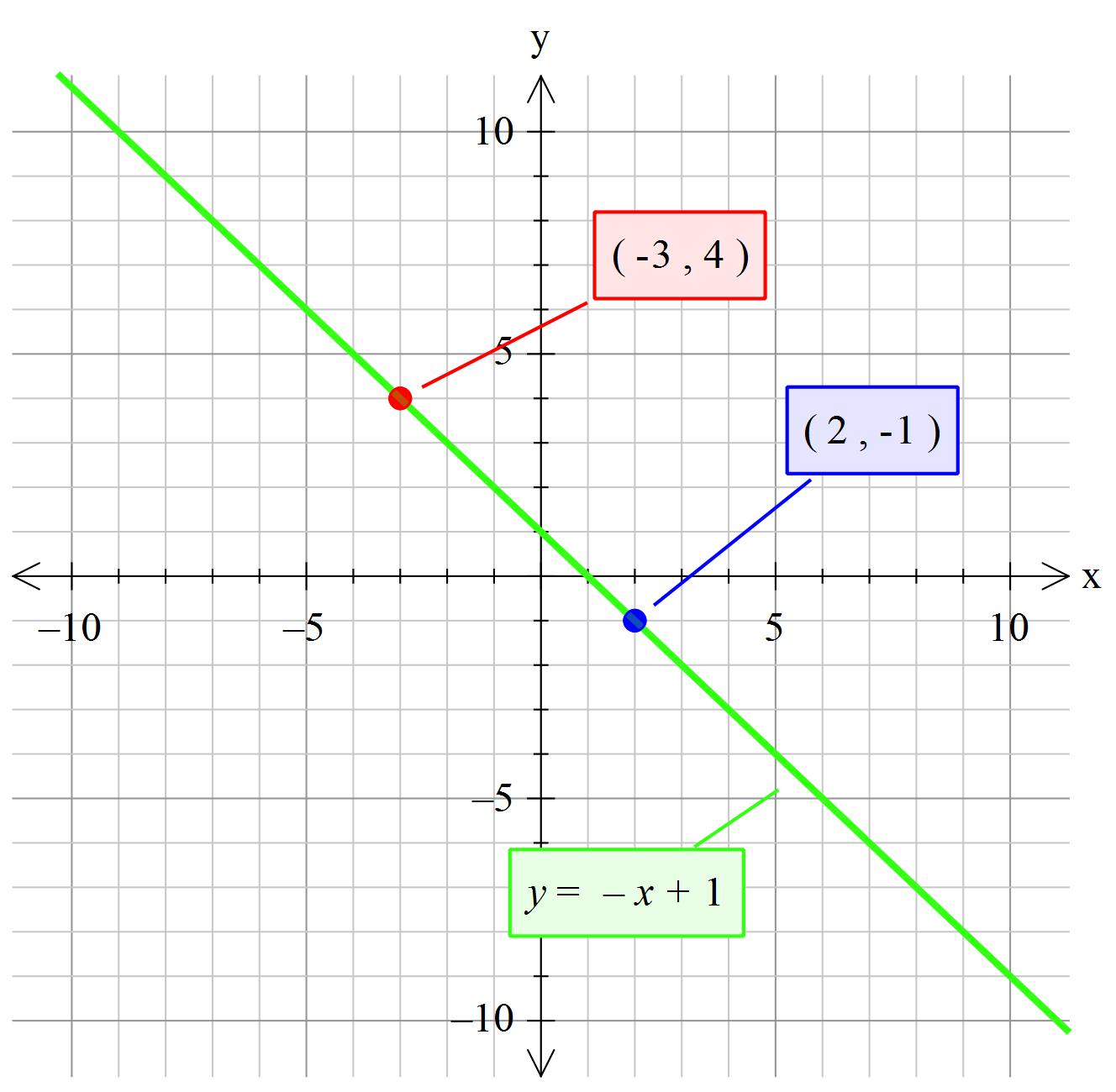
What is the slope-intercept form of the equation of the line that passes through the points (2, -1) and (-3, 4)?

Question

1375 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-04-05T14:35:50

#color(blue)(y=-x+1)#

#"standard form " -> y=mx+c#

Where #m# is the gradient and #c# is the #y_("intercept")#

#m=("change in y-axis")/("change in x-axis")#

Let point 1 be #P_1->(x_1,y_1) ->(2,-1)#
Let point 2 be# P_2->(x_2,y_2)->(-3,4)#

Then #m= (y_2-y_1)/(x_2-x_1) = (4-(-1))/(-3-2)#

#color(blue)(=>m=5/(-5) = -1)#

This means that as you move from left to right; for one along you go down 1 (negative incline).

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So the equation becomes

#color(brown)(y=-x+c)#

At #P_1"; "color(brown)(y=-x+c)color(green)( " "->" "-1=-2+c)#

#=> c= 2-1=1#

So the equation becomes

#color(blue)(y=-x+1)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~
Tony B