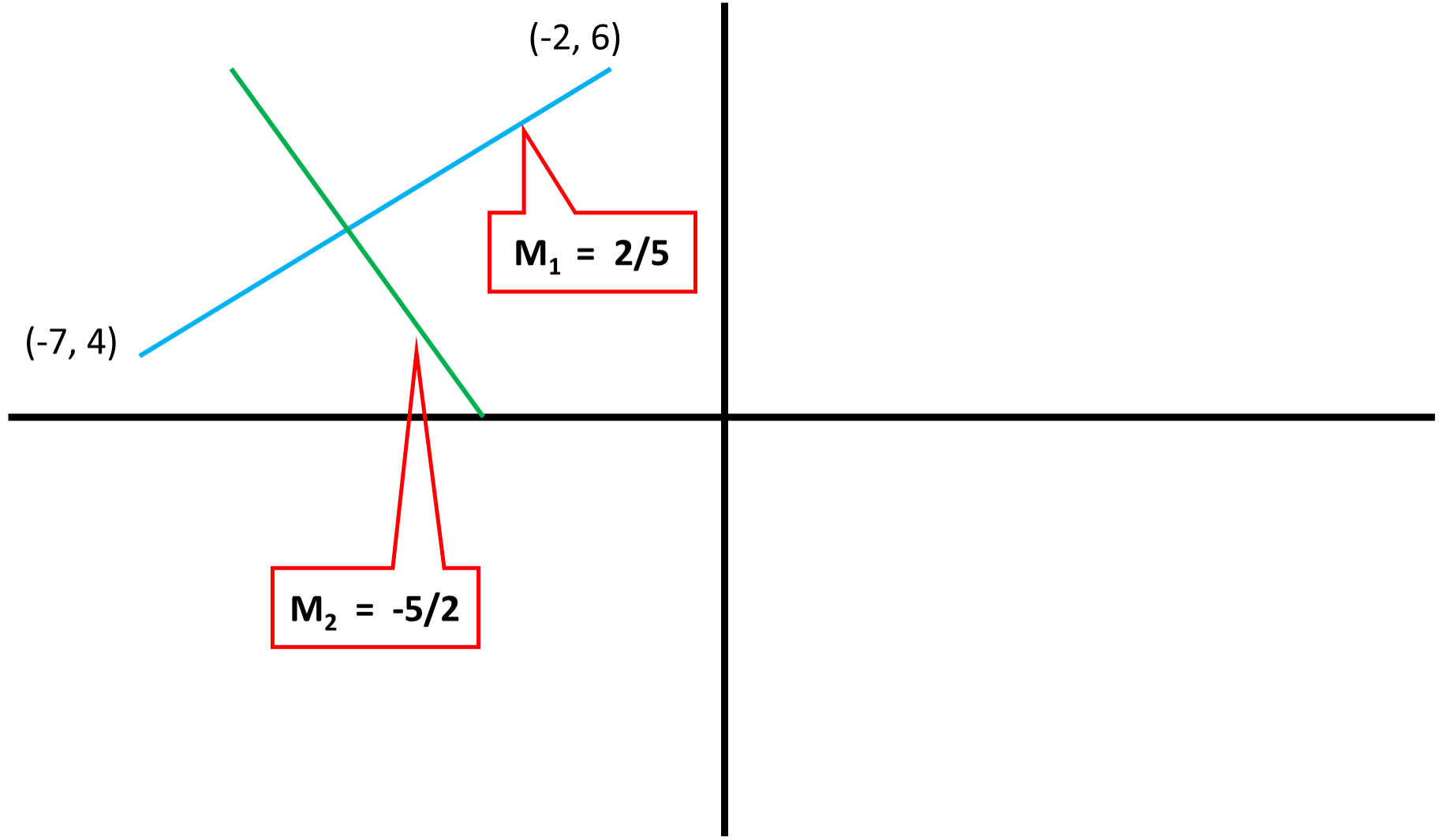
What is the slope of any line perpendicular to the line passing through #(-2,6)# and #(-7,4)#?
2 Answers
Apr 29, 2016
Slope of the perpendicular line
Explanation:
Given -
The two points on the given line.
#x_1=-2#
#y_1=6#
#x_2=-7#
#y_2=4#
Slope of the given line
#=(y_2-y_1)/(x_2-x_1)=(4-6)/(-7-(-2))=(-2)/(-5)=2/5#
Slope of the perpendicular line
Two line are perpendicular if
Find
#2/5 xx m_2= -1#
#m_2=-1 xx 5/2=-5/2#
Apr 29, 2016
Explanation:
Find slope of line through points using formula


