What is the slope of the line passing through # (-2,7); (9,1)#?
2 Answers
May 2, 2018
Explanation:
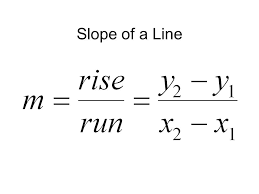
#m = -6 / 11
May 2, 2018
Slope:

