What is the slope of the tangent line of #(1-x)(4-y^2)-1/lny = C #, where C is an arbitrary constant, at #(1,2)#?
2 Answers
It is not possible to specify a value for C. See graph, with the line y = 2. and the explanation.
Explanation:
C is seemingly single-valued, but really not so.
It is so, upon setting x = 1 and y = 2 in the equation.
Here, C is shown as -1 /ln 2.
With this C for the graph ,the line y = 2 meets it at point(s) given by
The solution is x is arbitrary.
An attempt to find the equation to the virtual tangent at (1, 2) would
result in y = 2.
See the (y=2)-inclusive graph.
graph{(y-2+10^(-10)x)((x-1)(y^2-4)-1/ln y+1/ln 2)=0 [-10, 10, -5, 5]}
The slope is
Explanation:
Use implicit differentiation (or partial derivatives) to find
At
Given that
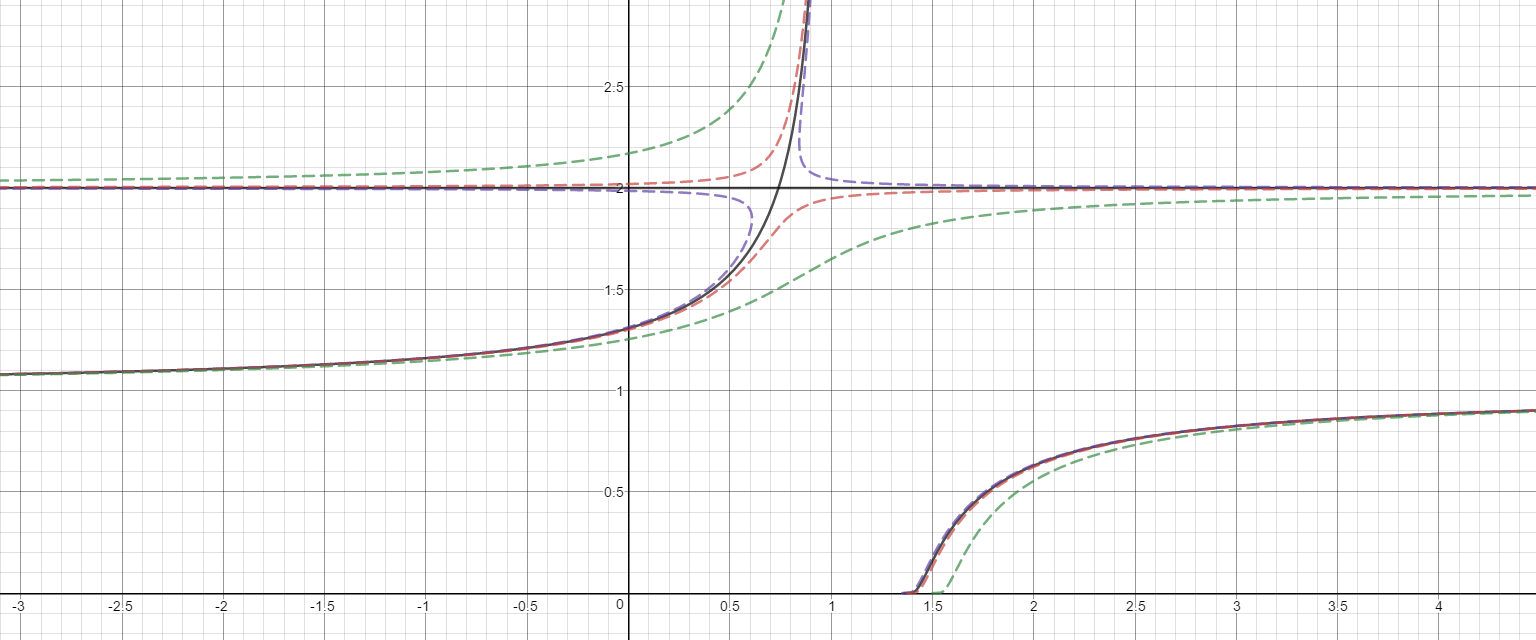
Here are some of the curves in this family.
red dots
red dash
blue dash
black dash
solid black
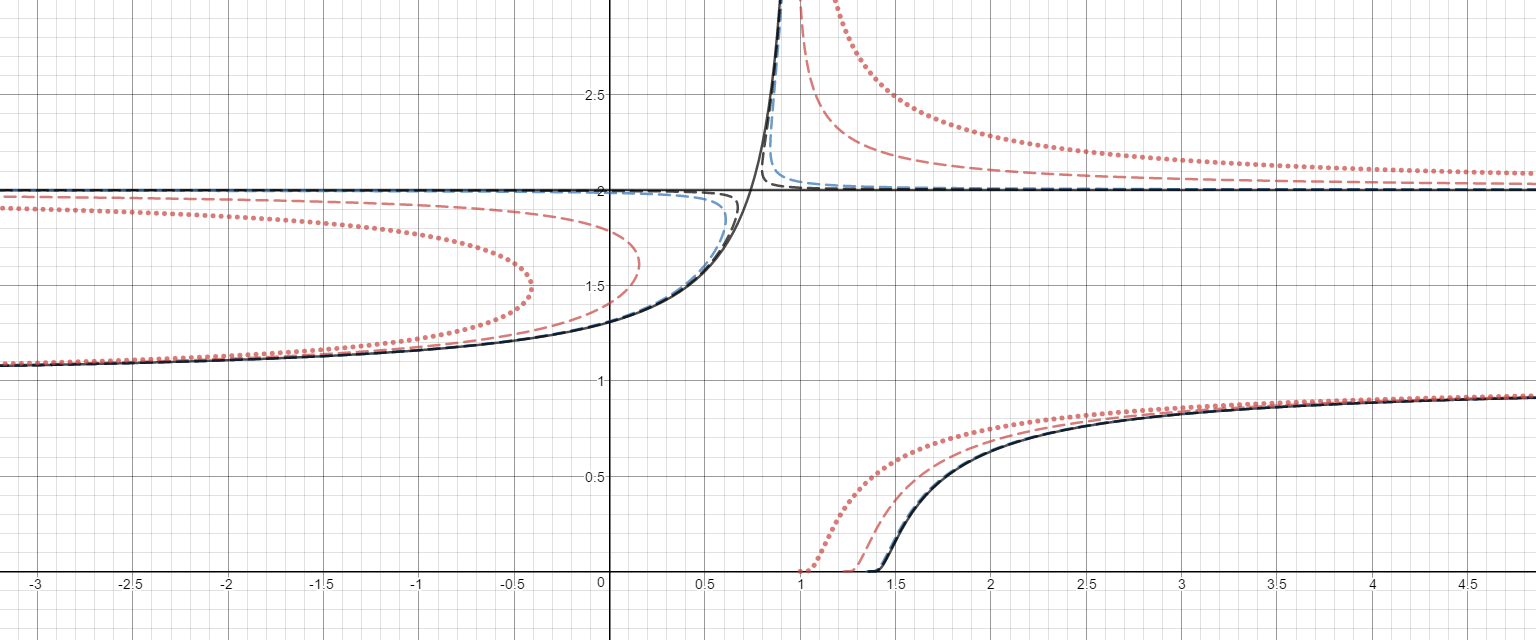
And here are the same near
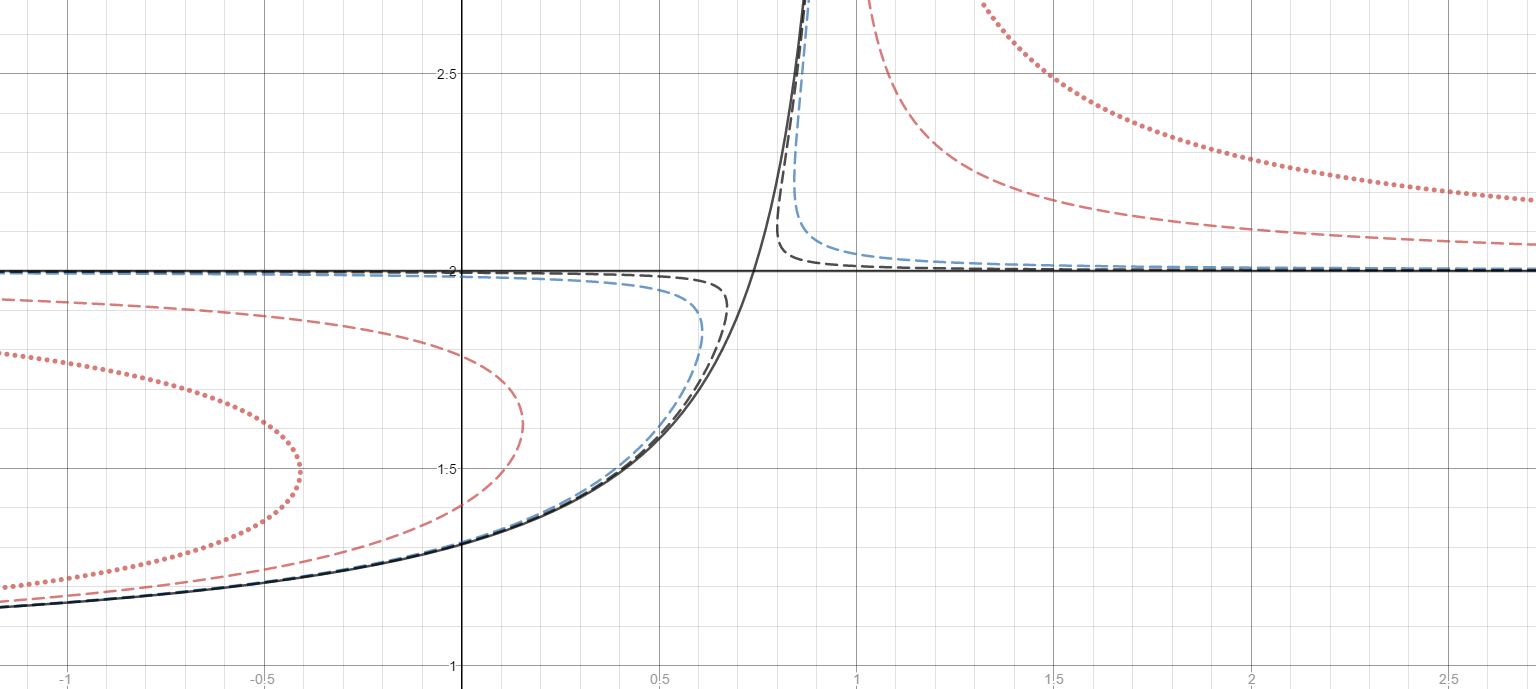
The point of at which the two branches meet appears to be
And if we continue with values of
blue dash
solid black
red dash
green dash