Given #p = (-2,1)# if this point pertains to the graphic of #f(x,y)=(x-y)^3e^y-C# then #f(-2,1)=0-> (-2-1)^3e^1-C=0# so #C = -27 e#.
Also from #(x-y)^3e^y=C# we obtain #x = (C e^{-y})^{1/3}+y#.
A generic point #p_0# pertaining to #f(x,y)=0# has the form
#p_0=((C e^{-y_0})^{1/3}+y_0,y_0)#.
Calculating #(dy)/(dx)# we proceed as:
#df(x,y)=f_xdx+f_ydy=0->(dy)/(dx)=-(f_x)/(f_y)# then
#(dy)/(dx) = 3/(3 - x + y) = 3/(3 - (C e^{-y})^{1/3})#
The tangent straight to the point #p_0# gives
#(y-y_0)=3/(3 - (C e^{-y_0})^{1/3})(x-x_0)# but
#x_0 = (C e^{-y_0})^{1/3}+y_0# so the tangent at #p_0# reads
#y = y_0 + 3/(3 - (C e^{-y_0})^{1/3})(x-(C e^{-y_0})^{1/3}+y_0)#
And for #p_0=(-2,1)# reads
#y=(12 e^(1/3) + 3 e^(1/3) x)#
/(6 e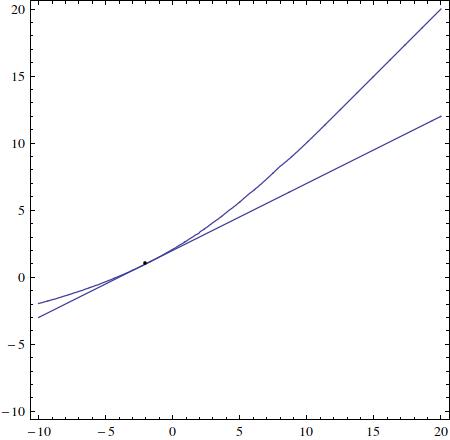 ^(1/3))#
^(1/3))#
 ^(1/3))#
^(1/3))#
