What is the slope of the tangent line of # (xy-y/x)(xy-x/y) =C #, where C is an arbitrary constant, at #(-2,1)#?

1 Answer
Steve M
Feb 1, 2017

The slope of the tangent is #0# at #(-2,1)#, But #(-2,1)# only lies on the curve in the specific case of #C=0#

Explanation:

We have:

# (xy-y/x)(xy-x/y) =C #

At #(-2,1)# we have:

# (-2+1/2)(-2+2) =C => C=0#

Multiplying out gives:

# (xy)(xy) - (xy)(x/y) - (xy)(y/x) + (y/x)(x/y) = C#
# x^2y^2 - x^2 - y^2 + 1 = C#

Differentiating wrt #x# (Implicitly and using the product rule):

# (x^2)(2ydy/dx) + (2x)(y^2) -2x - 2ydy/dx = 0 #
# :. x^2ydy/dx + xy^2 -x - ydy/dx = 0 #
# :. (x^2y-y)dy/dx + xy^2 -x = 0 #
# :. (x^2y-y)dy/dx = x - xy^2 #
# :. dy/dx = (x - xy^2)/(x^2y-y) #

So at #(-2,1)# we have:

# :. dy/dx = (-2 - (-2))/(4-1) = 0#

So the slope of the tangent is #0# at #(-2,1)#, But #(-2,1)# only lies on the curve in the specific case of #C=0#

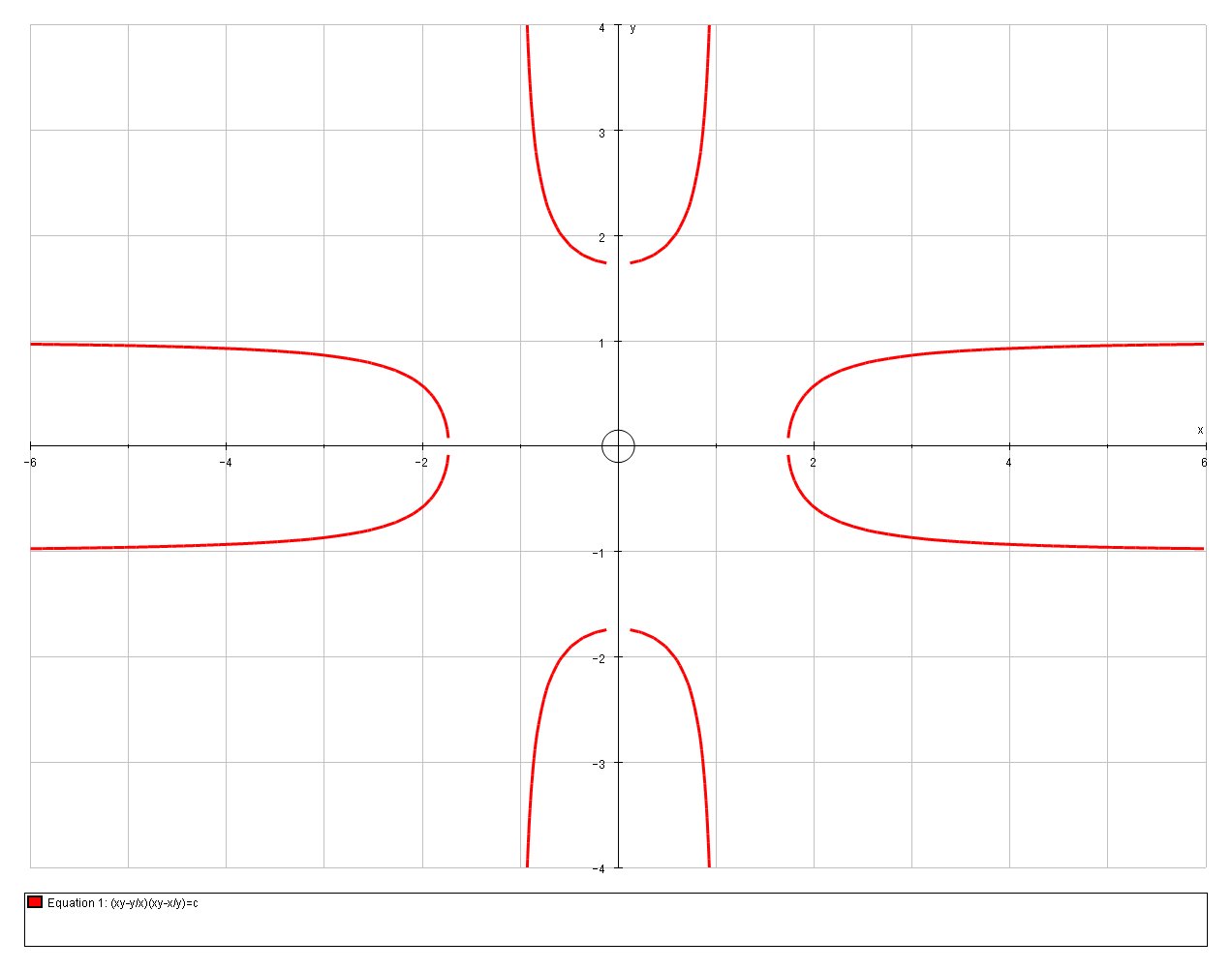
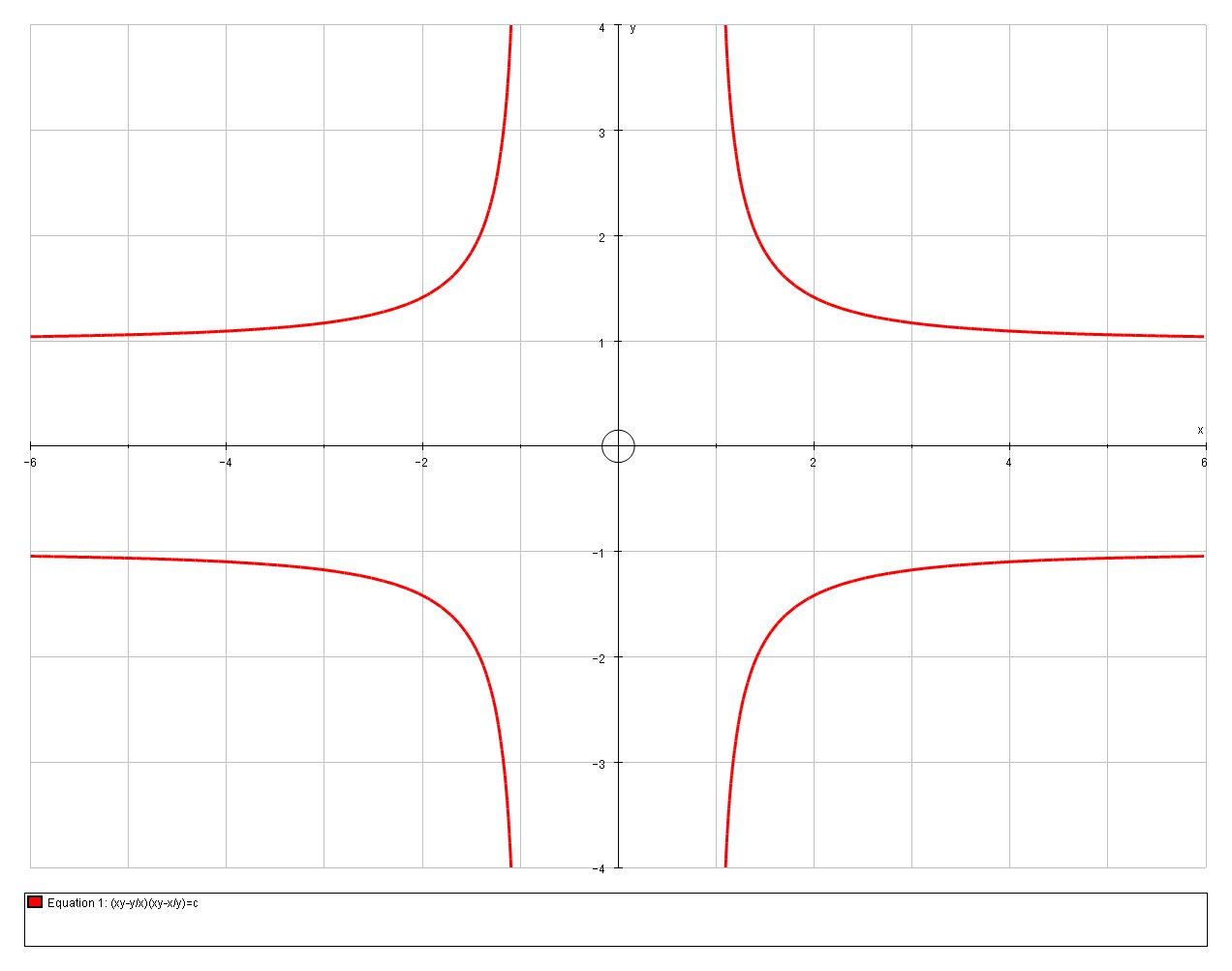
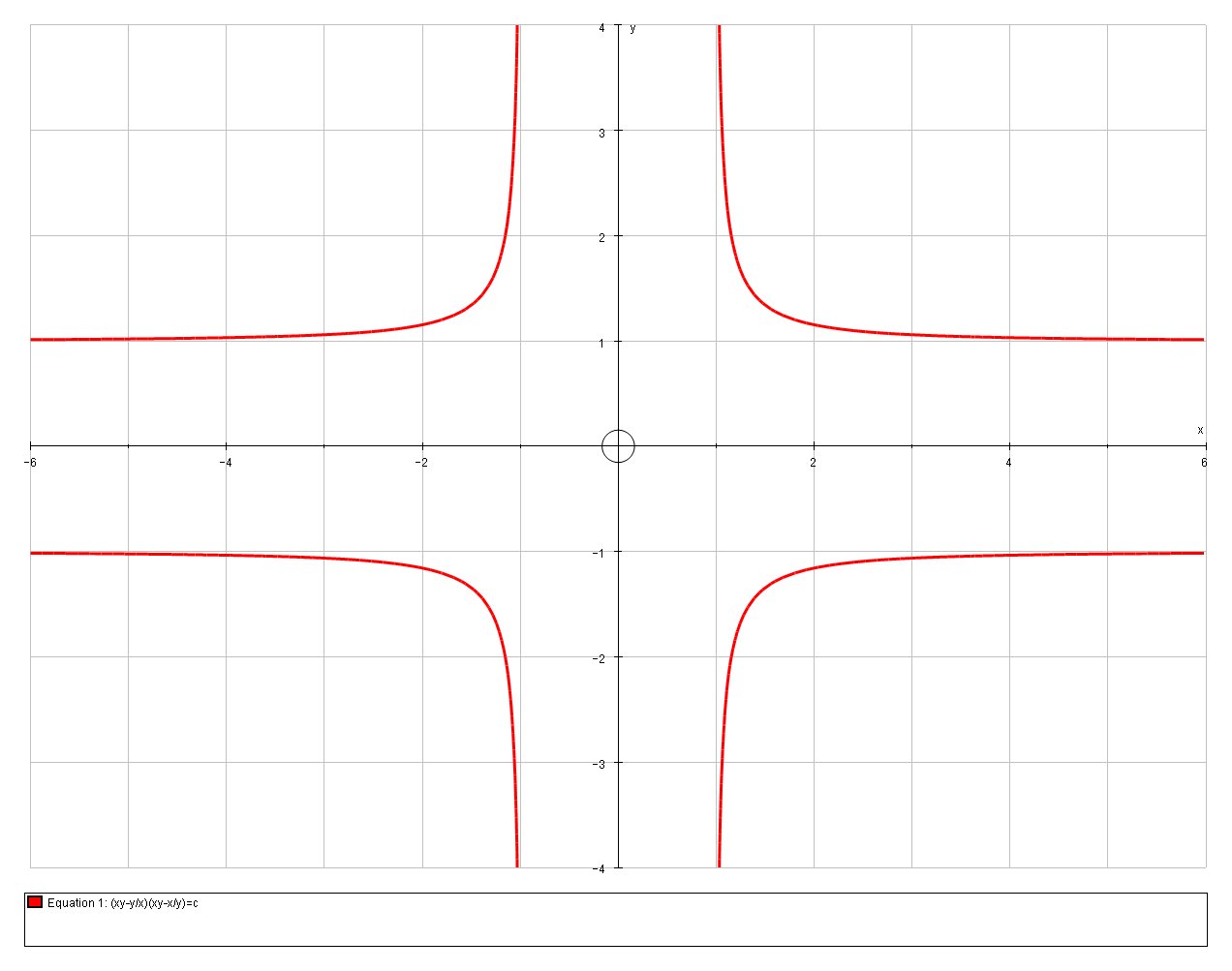
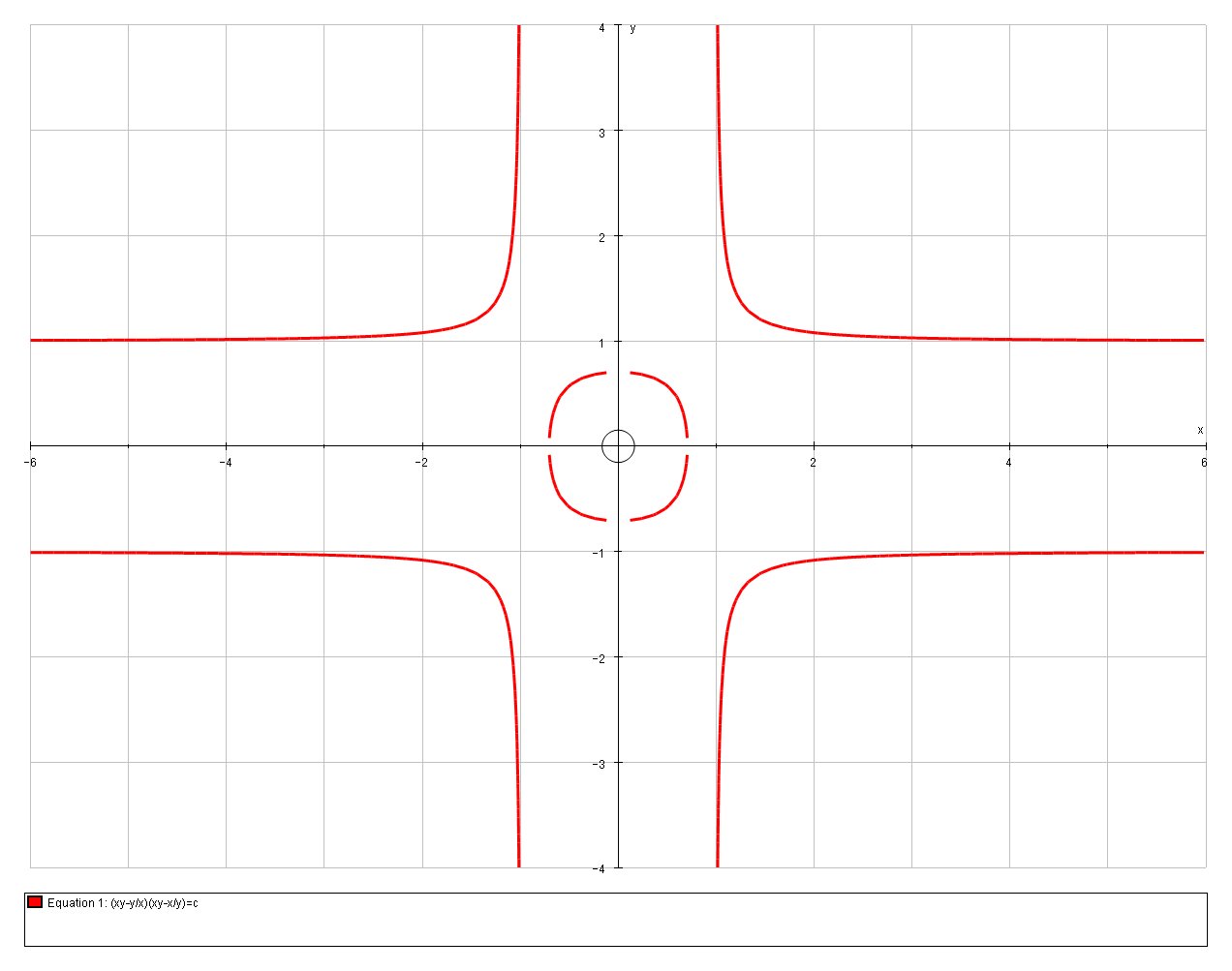
The curve of this family are quote interesting:

C=3
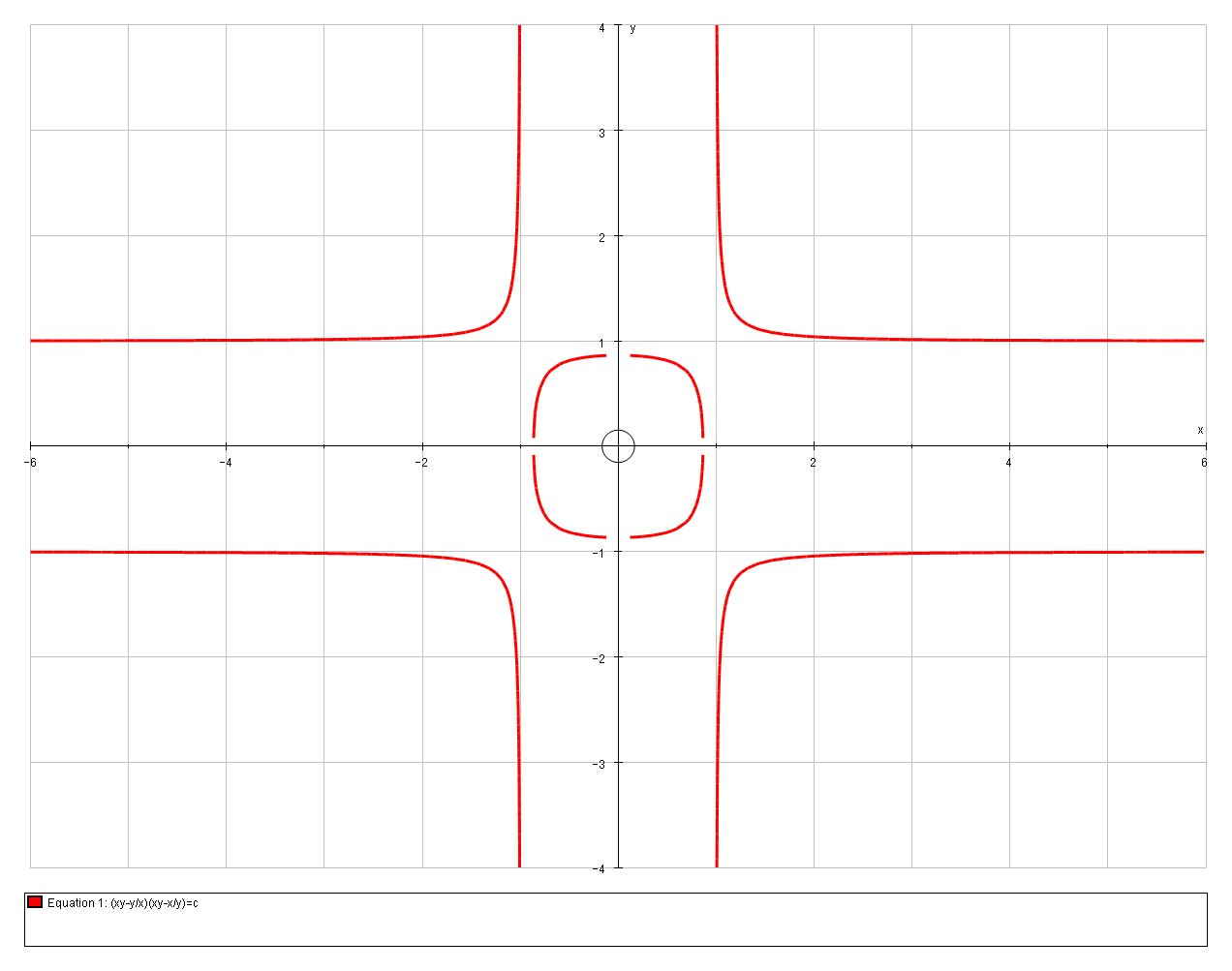
enter image source here

C=1
enter image source here

C=0.5
enter image source here

C=0.25
enter image source here

C=0 - The specific curve that (-2,1) lies on
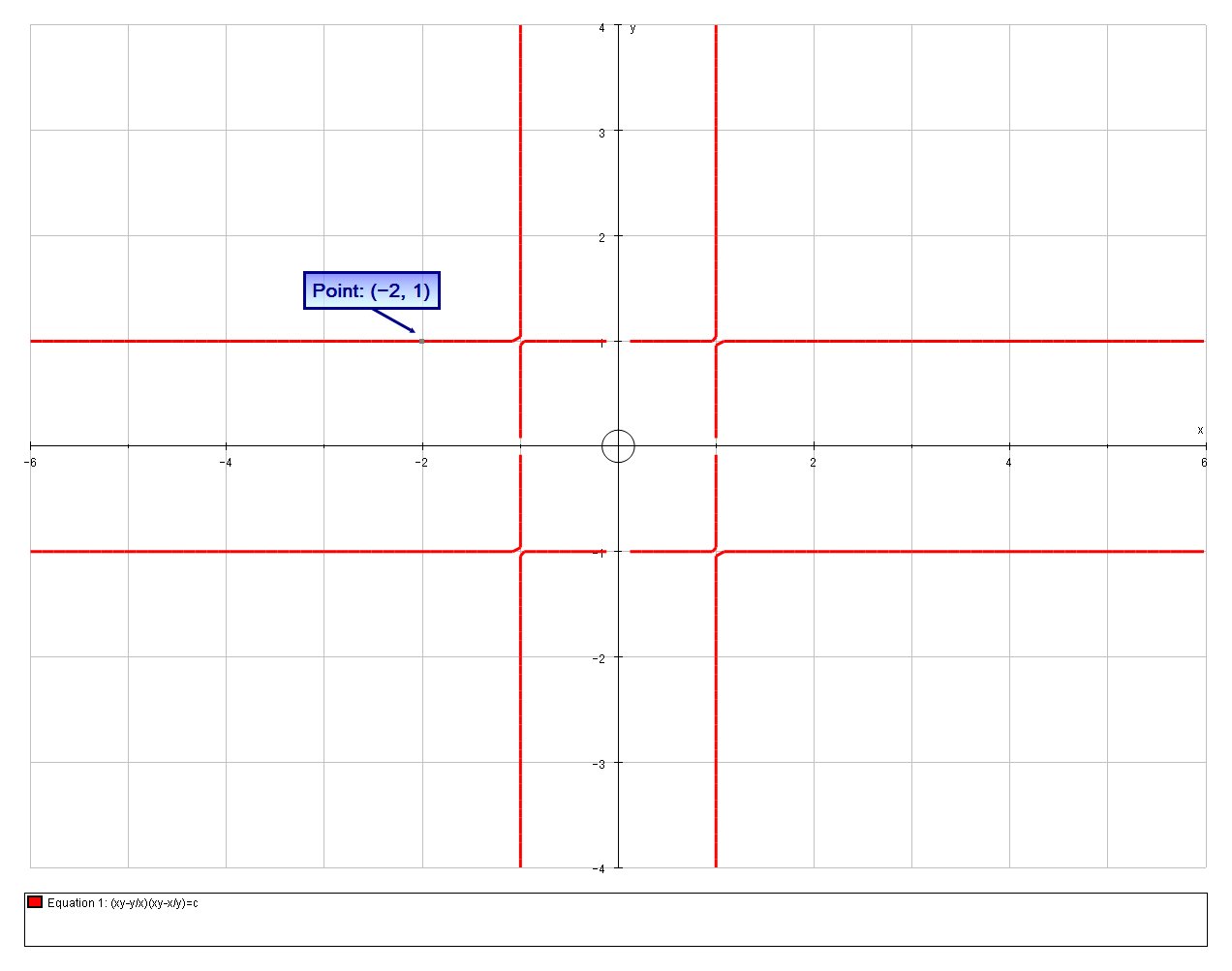
enter image source here

C=-1
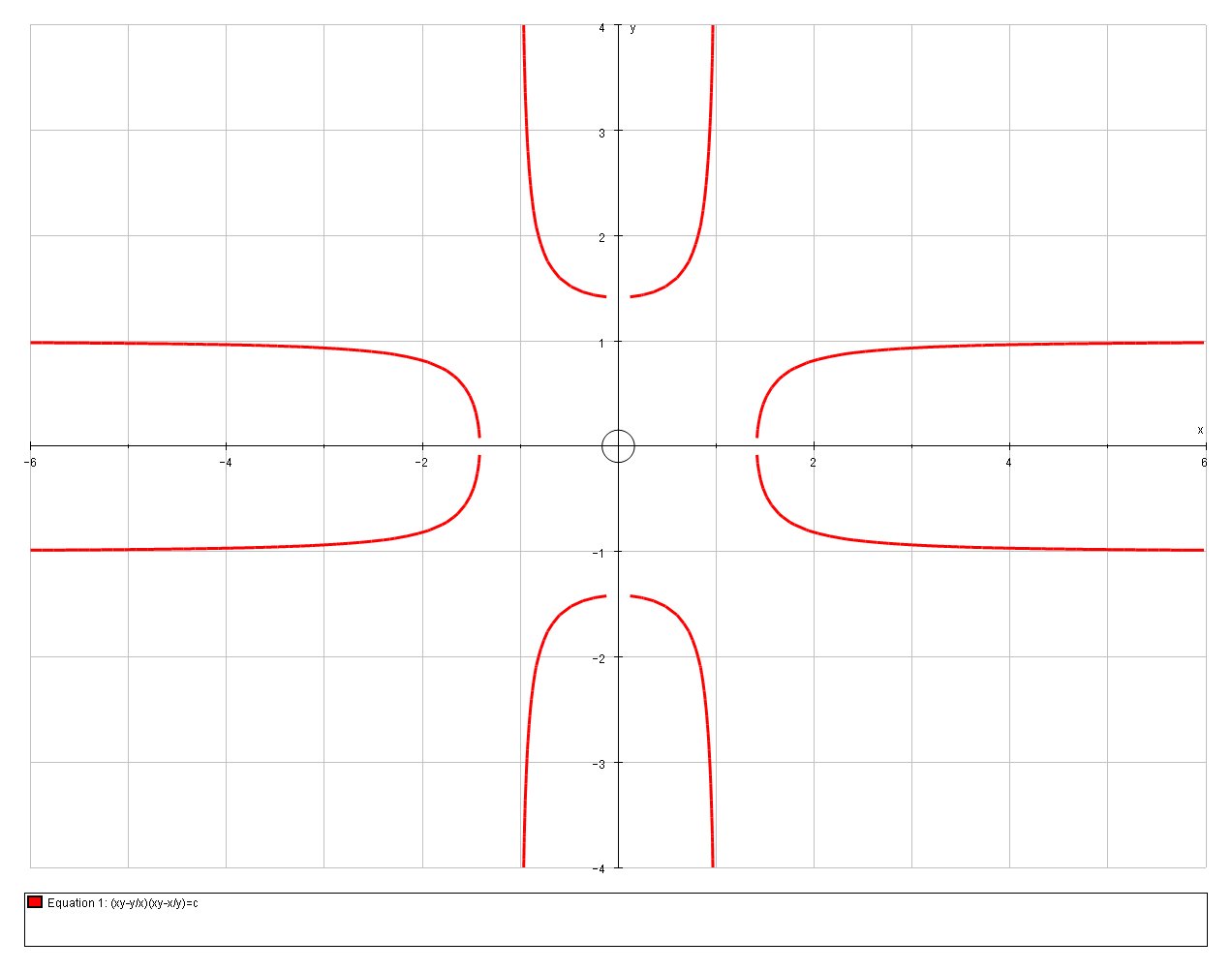
enter image source here

C=-2
enter image source here

Related questions
See all questions in Implicit Differentiation
Impact of this question
1124 views around the world
You can reuse this answer
Creative Commons License