Question

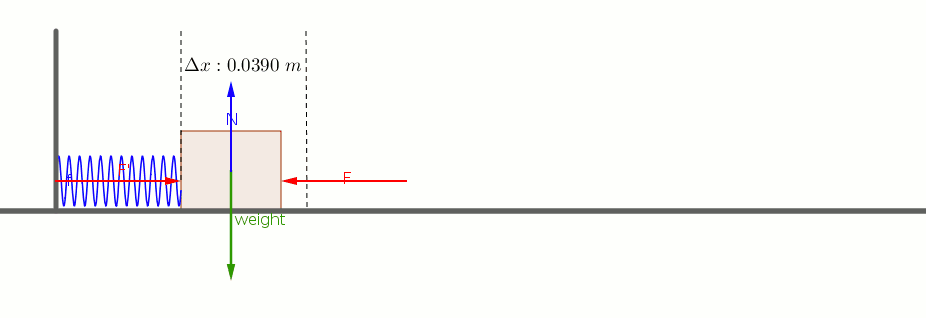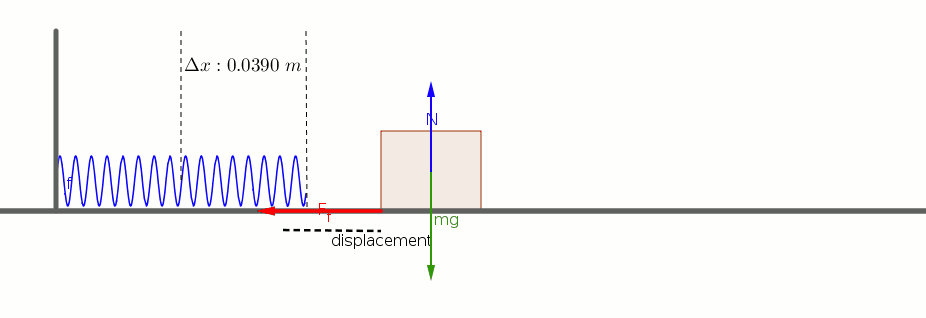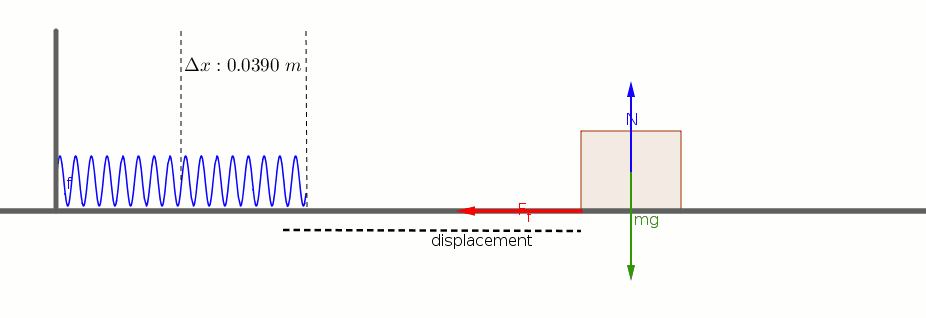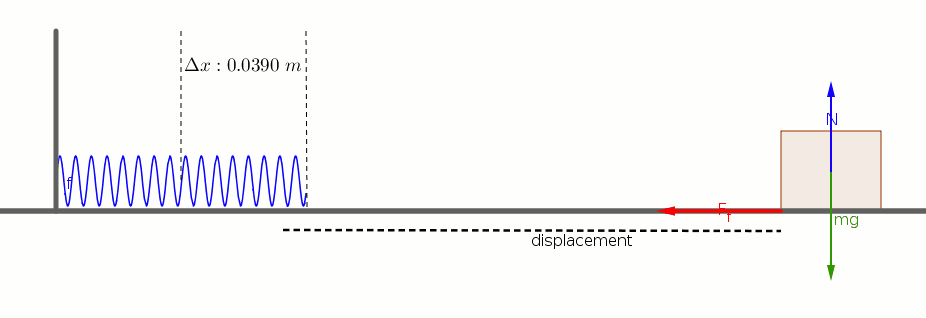
What is the speed of the block when it has moved a distance of 0.0200 m from its initial position? (At this point the spring is compressed 0.0190 m). See details.

A 2.55 kg block on a horizontal floor is attached to a horizontal spring that is initially compressed 0.0390 m. The spring has a force constant of 815 N/m. The coefficient of kinetic friction between the floor and the block is 0.35. The block and spring are released from rest and the block slides along the floor.

Answer 1

`v=0.32" "m/s`

Explanation:

`"When a spring is compressed by a Force of F,The potential energy "` `"is stored on it."`

`"if the spring is released, the Potential energy turns into kinetic energy."`

`"The object is repulsed by the call-back force which occurs on the spring"`

`F'=K*Delta x`

`K=815 N/m`
`Delta x=0.0190" "m`

`F'=815*0.019=15.48" "N`

`F_f=k*m*g`

`F_f=0.35*2.55*9.81=8.76N" Friction force"`

`"acceleration of object is :"`

`a=(F'-F_f)/m`

`m=2.55kg" mas of object"`

`a=(15.48-8.76)/(2.55)`

`a=2.64" "m/s^2`

`v^2=2*a*displacement`

`v^2=2*2.64*0.0200`

`v^2=0.1056`

`v=sqrt(0.1056)`

`v=0.32" "m/s`