Question

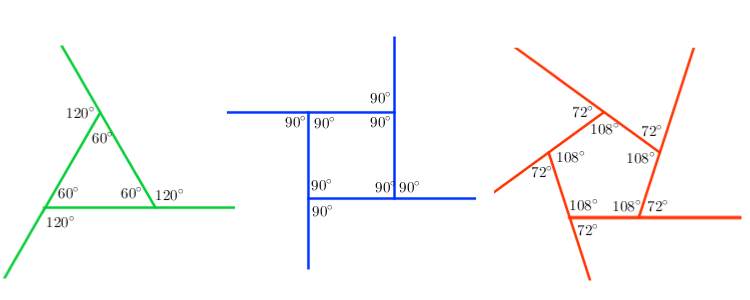
What is the sum of the measures of the interior angles of a regular polygon where a single exterior angle measures 72°?

Answer 1

The sum of the interior angles would be `540^o`

Explanation:

If the regular polygon has an exterior angle of `72^o` this means there would be 5 sides to the polygon and it would be a pentagon.

The exterior measures of a polygon must add up to `360^o`, therefore `360^o / 72^o` would mean 5 exterior angles, five interior angles and therefore 5 sides to the polygon. (see diagram below)

The exterior angle and the interior angle of any polygon are supplementary and must add up to `180^o`.

`180^o - 72^o = 108^o`
Each interior angle would therefore be `108^o`

Since there are 5 angle in a pentagon `5x108^o = 540^o`