What is the term used for a well insulated reaction vessel used to measure delta H of reactions?
1 Answer
Often the determination of the enthalpy of reaction can be done in a coffee-cup calorimeter, otherwise known as a constant-pressure calorimeter.
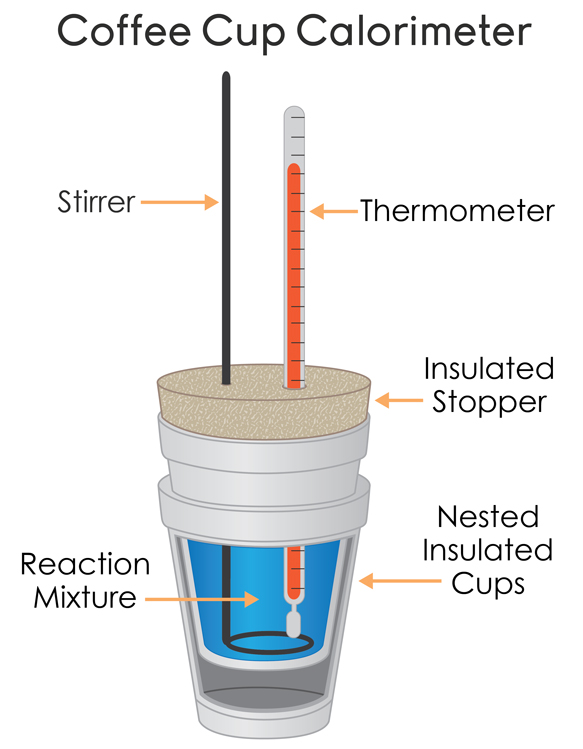
This device is often well-insulated so that we can rightfully say,
#q_(soln) ~~ -q_(rxn)#
That is,
At constant pressure, the heat flow through the solution,
This heat flow came out into the solution due to the reaction, so by conservation of energy,
#color(blue)(q_(soln)/(n_("product")) = -DeltabarH_(rxn))# ,for the relationship through which one can find the enthalpy of a reaction that occurs in a solution inside the coffee-cup calorimeter, where
#n_("product")# is the mols of the reaction product.
For the solution heat flow, we write:
#q_(soln) = m_(soln)C_(soln)DeltaT# ,
and we often approximate the solution heat capacity
The mass of the solution,
Thus, by measuring the temperature change in the solution, and knowing how much solution was measured out, one can determine

