Question

What is the unit vector that is orthogonal to the plane containing `(-2i- 3j + 2k)` and `(3i – 4j + 4k)`?

Answer 1

Take the cross product of the 2 vectors
`v_1 = (-2, -3, 2) and v_2 = (3, -4, 4)`
Compute `v_3 = v_1 xx v_2`
`1/sqrt(501) (-4, 14, 17)`

Explanation:

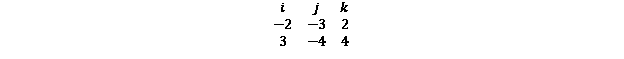
The `v_3 = (-4, 14, 17)`
The magnitude of this new vector is:
`|v_3| = 4^2 + 14^2 + 17^2`
Now to find the unit vector normalize our new vector
`u_3 = v_3/ (sqrt( 4^2 + 14^2 + 17^2)); = 1/sqrt(501) (-4, 14, 17)`