Question

What is the unit vector that is orthogonal to the plane containing `( i - 2 j + 3 k)` and `( - 5 i + 4 j - 5 k)`?

Answer 1

`= 1/sqrt(35)<1,5,3>`

Explanation:

you need to calculate the vector (cross) product of these two vectors to get the normal vector

it's not clear to me how you latex matrices on here so i will draw the computation.

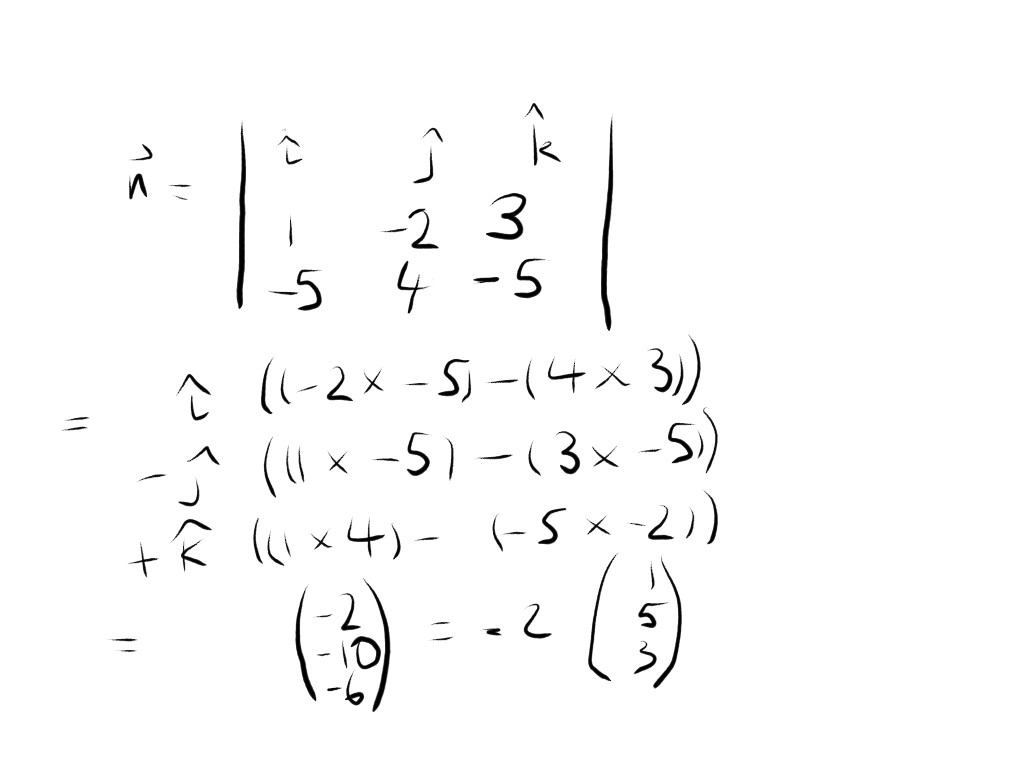
so the normal vector is the determinant of the matrix as shown and we get as one possible normal vector [there an an infinite number of actual formulations of this]

`vec n = <1,5,3>`

the unit vector is therefore

`hat n = 1/sqrt(1^2 + 5^2 + 3^3)<1,5,3>`

`= 1/sqrt(35)<1,5,3>`

or

`= - 1/sqrt(35)<1,5,3>` pointing in other direction