The volume is \frac{81\sqrt{3}}{40}\approx 3.507481√340≈3.5074.
The curve y=-x^2+5x-4=-(x-1)(x-4)y=−x2+5x−4=−(x−1)(x−4) has xx-intercepts at x=1x=1 and x=4x=4 (and is above the xx-axis for 1<x<41<x<4).
For 1< x< 41<x<4, let b(x)=-x^2+5x-4b(x)=−x2+5x−4. This will be the base of the equilateral triangle cross-section at xx.
The solid itself looks something like this:
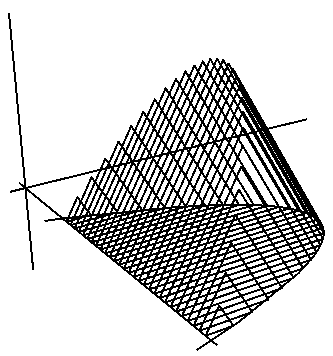
Now draw the cross-section equilateral triangle, label the sides b(x)b(x), and draw a vertical line for the height h(x)h(x) from the top vertex down perpendicular to the base.
By the Pythagorean Theorem, (b(x))^2=(\frac{b(x)}{2})^2+(h(x))^2(b(x))2=(b(x)2)2+(h(x))2.
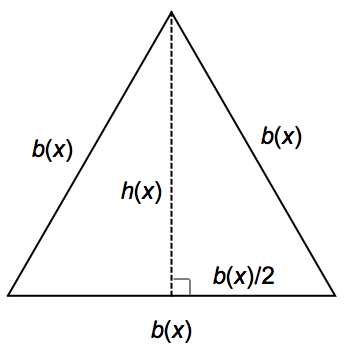
so that h(x)=\sqrt{(b(x))^2-(\frac{b(x)}{2})^2}=\sqrt{\frac{3}{4}(b(x))^2}=\frac{\sqrt{3}}{2}b(x)h(x)=√(b(x))2−(b(x)2)2=√34(b(x))2=√32b(x).
The cross-sectional area is A(x)=\frac{1}{2}b(x)h(x)=\frac{\sqrt{3}}{4}(b(x))^2=\frac{\sqrt{3}}{4}(x^{4}-10x^{3}+33x^{2}-40x+16)A(x)=12b(x)h(x)=√34(b(x))2=√34(x4−10x3+33x2−40x+16), which means the volume of the solid is V=\int_{1}^{4}A(x)dx=\frac{\sqrt{3}}{4}\int_{1}^{4}(x^{4}-10x^{3}+33x^{2}-40x+16)dx=\frac{\sqrt{3}}{4}(\frac{x^{5}}{5}-\frac{5x^{4}}{2}+11x^{3}-20x^{2}+16x)|_{x=1}^{x=4}V=∫41A(x)dx=√34∫41(x4−10x3+33x2−40x+16)dx=√34(x55−5x42+11x3−20x2+16x)∣∣∣x=4x=1.
Continuing to simplify gives V=\frac{\sqrt{3}}{4}((\frac{1024}{5}-\frac{1280}{2}+704-320+64)-(\frac{1}{5}-\frac{5}{2}+11-20+16))=\frac{\sqrt{3}}{4}(\frac{64}{5}-\frac{47}{10})=\frac{81\sqrt{3}}{40}V=√34((10245−12802+704−320+64)−(15−52+11−20+16))=√34(645−4710)=81√340.




