An oxygen atom has a total of 8 elections. How do you write the 4 quantum numbers for each of the 8 electrons in the ground state ?
2 Answers
You know that a neutral oxygen atom has 8 electrons.

It's always helpful to write the electron configuration for an element before trying to assign quantum numbers for each individual electron . As you can see in the image above, the electron configuration for neutral oxygen is
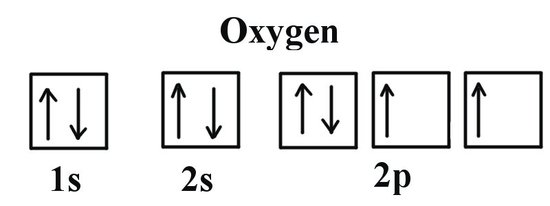
Assuming you know the basics behind quantum numbers, you can write the unique 4-number set for each electron belonging to oxygen like this
The first energy level:
The second energy level:
First, you must know the rules for quantum numbers.
Explanation:
Then you use the Aufbau Principle, the Pauli Exclusion Principle, and Hund's Rule to assign the quantum numbers.
The rules for quantum numbers are:
No two electrons can have the same set of four quantum numbers.
According to the Aufbau Principle, electrons fill orbitals starting at the lowest possible energy levels.
So the first two electrons have the quantum numbers
The Pauli Exclusion Principle states that no two electrons in the same atom can have the same set of four quantum numbers.
So the next two electrons have the quantum numbers
Now Hund's Rule comes into effect.
Hund's Rule states that if two or more orbitals of equal energy are available, electrons will occupy them singly and with the same spin before filling them in pairs.
The next four electrons have the quantum numbers
And now you have the quantum numbers for the eight electrons in an oxygen atom.


