What is the z-score of sample X, if #n = 256, mu= 67, St. Dev. =80, and mu_X =56#?

1 Answer
Jorge G. Pires
Apr 22, 2016

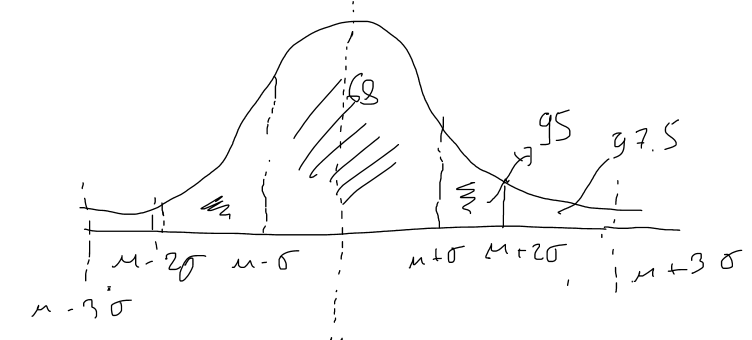
It is -2.2. That means that you are between 95-97% of the curve probability density function.

Explanation:

Theorem for z-score calculation, from Logan, J. David and Wolesensky, Willian R. Mathematical methods in biology. Pure and Applied Mathematics: a Wiley-interscience Series of Texts, Monographs, and Tracts. John Wiley& Sons, Inc. 2009.
It is -2.2000. That means that you are between 95-97% of the curve probability density function.

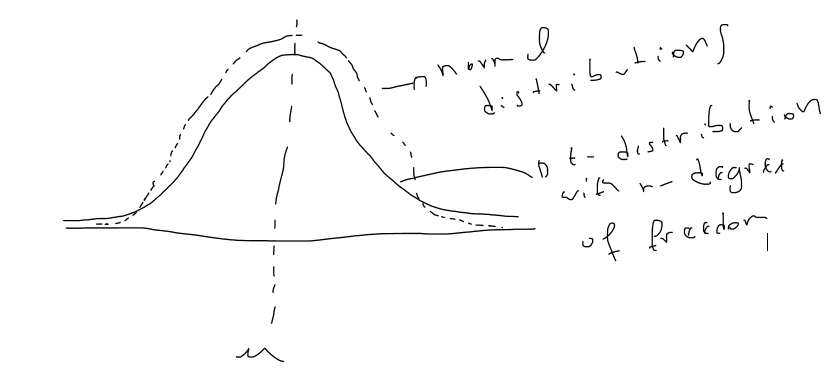
It is calculated using, assuming you random variable is normal, otherwise you should use the t-student, which is similar, but with a "fatter" tale:

#z=(mu_X - mu)/(sigma/sqrt(n))#, which is a normal distribution with mean 0 and standard deviation 1. I have used #sigma=#standard deviation

This formula is value for N samples from a normally distributed random variable, with known stDev and meam, which was given in the question heading.

In this scheme, you see a famous thumb rules, 1-2-3-> 68-95-95.7, which means that if you have a z-score equals 1, you are within 68% of the curve. Remember that it is symmetric, thus this probability interpretation is for the two tales. That means in practical terms, the probability of falling 2 standard deviation is 95%, but between 2, is 17% against 68% for one standard deviation.

normal distribution against the student one

Code used to calculate the score in Matlab

See also
* z-scores in Matlab

Related questions
See all questions in One-sample z test
Impact of this question
4164 views around the world
You can reuse this answer
Creative Commons License