Question

What Is Z component of orbital angular momentum? How can we find the Z component? What is its importance? What does it resemble?

Answer 1

You seem to be referring to `m_l`, which is the observed value that corresponds to the `z`-component of the total orbital angular momentum `L_z`.

Practically speaking, for general chemistry, you can simply use the value of `l` as the range of `m_l`, and express `m_l` as:

`bb(m_l = {-l,-l+1, . . . , 0, . . . , l - 1, l})`

For instance, if `l = 2` (as for a `d` orbital), then:

`m_l = {-2,-1,0,+1,+2}`

That means five `d` orbitals exist for a given principal quantum number `n`:

---

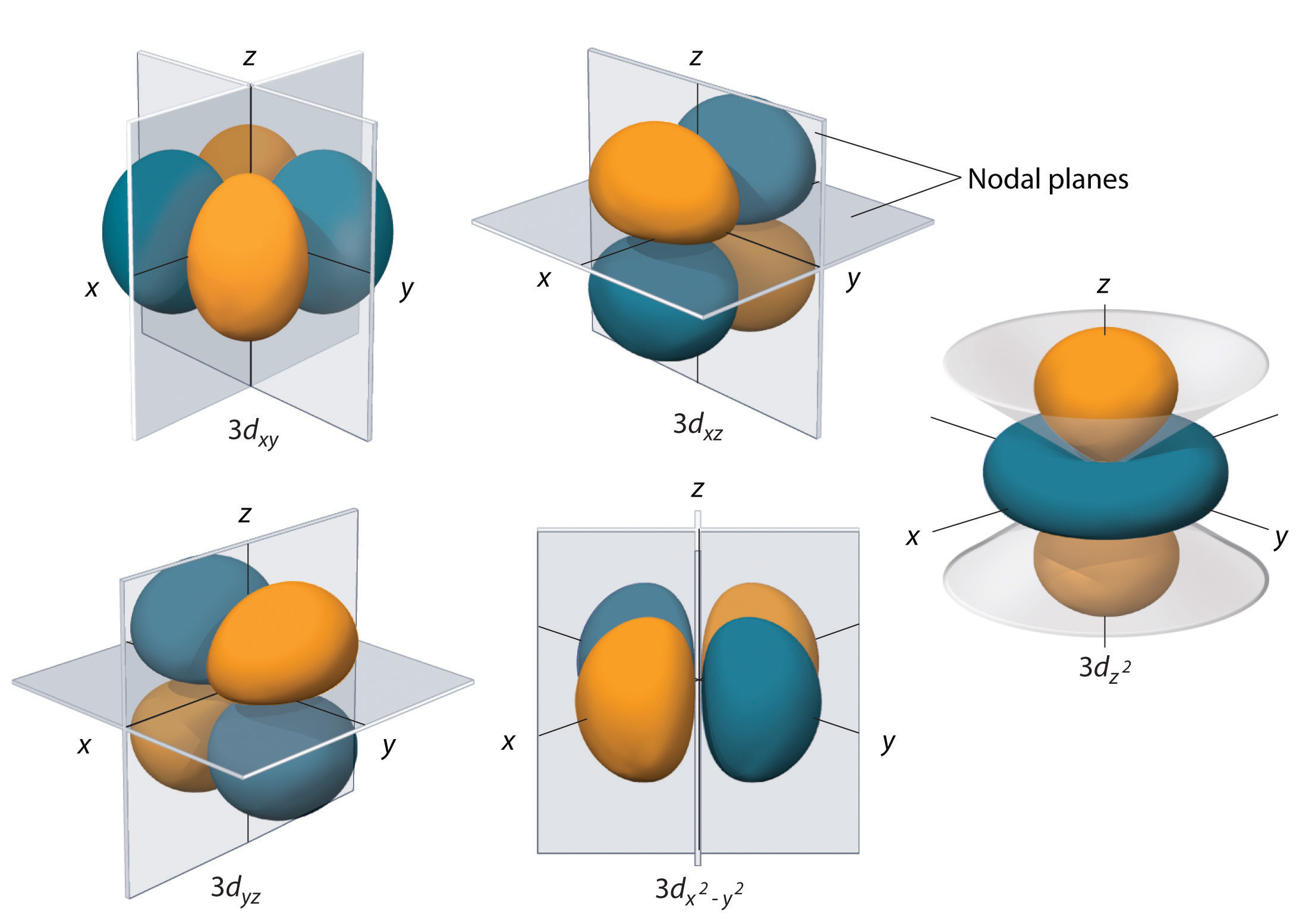
RELATION TO THE Z-COMPONENT OF THE TOTAL ORBITAL ANGULAR MOMENTUM

Recall that the Schrodinger equation is typically written as `hatHpsi = Epsi` (where `E` is the energy, `hatH` is the Hamiltonian operator, and `psi` is the wave function).

Well, it turns out that `psi`, the wave function describing the state of a quantum mechanical system, can be separated into a radial and an angular component, `R_(nl)(r)` and `Y_(l)^(m_l)(theta,phi)`:

`psi_(nlm_l)(r,theta,phi) = R_(nl)(r)Y_(l)^(m_l)(theta,phi)`

where `n`, `l`, and `m_l` are the principal, angular momentum, and magnetic quantum numbers, respectively.

Traditionally, `m_l` is defined to be the `z` component of the angular momentum `l`, and it is the eigenvalue (the quantity we expect to see over and over again), in units of `ℏ`, of the wave function, `psi`.

This eigenvalue corresponds to the operator for `L_z`, and `L_z` is the `bb(z)` component of the total orbital angular momentum.

What we just said can be expressed as:

`stackrel("Operator")overbrace(hatL_z)" "stackrel("Angular")stackrel(" Component")stackrel("of Wave Function")overbrace(Y_(l)^(m_l)(theta,phi)) = stackrel("Eigenvalue")overbrace(m_lℏ)" "stackrel("Angular")stackrel(" Component")stackrel("of Wave Function")overbrace(Y_(l)^(m_l)(theta,phi))`

If `L_z` is what you mean, then the significance of it is that it is the phenomenon we can observe that corresponds to the magnetic quantum number `m_l`.

PHYSICS PERSPECTIVE

Visually, in the presence of a magnetic field in the `z` direction, a nuclear rotation (exhibiting a total orbital angular momentum) occurs along the `z` axis, called a "Larmor precession".

This is the event described by `L_z`.

For instance, when `l = 1`, as for a `p` orbital, `m_l = {-1,0,+1}`. The "Larmor precession" that occurs looks like the following for a `2p_z` orbital:

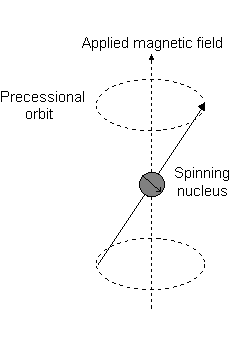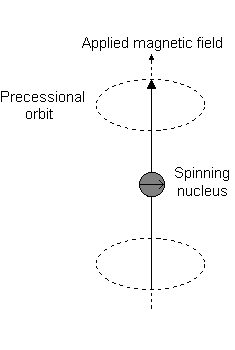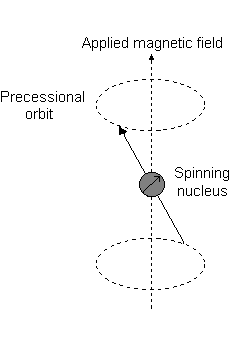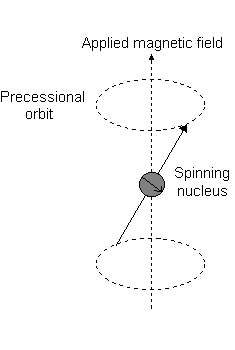
And each `m_l` corresponds to the distance from the `z` axis in units of `ℏ`:

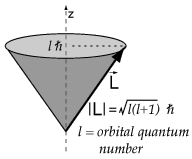
For instance:

• An `m_l` of `1` corresponds to the upper half of the `2p_z` orbital.
• An `m_l` of `0` is the dot at the origin.
• An `m_l` of `-1` corresponds to the lower half.

CHEMISTRY PERSPECTIVE

From a practical point of view, what we really care about is how to use `m_l`. Each `m_l` corresponds to a unique orbital in a particular subshell. So:

• The number of `m_l` values tells you the number of orbitals in a subshell.
• The range of `m_l` is based on the chosen `l`.

For example, since `l = 2` is for a `d` subshell, then:

`m_l = {-2,-1,0,+1,+2}`

That means five `d` orbitals exist for a given principal quantum number `n`: