What should I study to know how to solve?
I'm studying for a test, and they have several questions I've never dealt with, and I don't even know what the topics I should study are. Here are some of them:
cos δ = 1 , which of the following could NOT be a value of δ ?
Which of the following is equivalent to 2sin2θ+(1–cos2θ)/(tan2θ) ?
If sin∂=sqrt32 , what is the value of cot∂ ?
All that I want to know is WHAT I SHOULD STUDY to know how to solve these type of questions, since I have no idea how to even tackle them. I don't actually need the answers, just the names of the methods. Thanks!
I'm studying for a test, and they have several questions I've never dealt with, and I don't even know what the topics I should study are. Here are some of them:
Which of the following is equivalent to
If
All that I want to know is WHAT I SHOULD STUDY to know how to solve these type of questions, since I have no idea how to even tackle them. I don't actually need the answers, just the names of the methods. Thanks!
1 Answer
For the first question, know your unit circle and special angles. Here is an image:
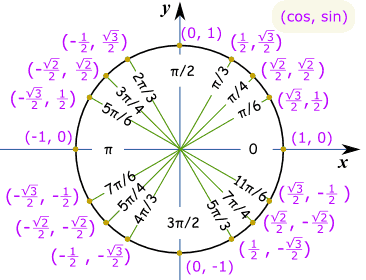 https://www.mathsisfun.com/geometry/unit-circle.html
https://www.mathsisfun.com/geometry/unit-circle.html
So if
For the second, you need to know your trig identities. Here is a picture of those that I think are most necessary to learn.
http://carbon.materialwitness.co/trig-identities/
We can simplify as
2(2sinthetacostheta) + (1 -(1 - 2sin^2theta))/((tan theta + tan theta)/(1 - tanthetatantheta)
4sinthetacostheta + ((2sin^2theta)(1 -tan^2theta))/(2tantheta)
4sinthetacostheta + (2sin^2theta - 2sin^2thetatan^2theta)/(2tantheta)
4sinthetacostheta+ sin thetacostheta- sin^2thetatantheta
5sinthetacostheta - sin^3theta/costheta
A lot of expressions cancel to things like
As for the last problem, this example is implausible as
Now from above you can see that
1 +cot^2alpha = 32
cot^2alpha = 31
cotalpha= +-sqrt(31)
If they clarify that
Hopefully this helps, please ask if you have any further questions!

