Question

What uses do products of power series have?

Answer 1

One example that I find useful is the use and manipulation of the products of power series to derive `e^(ix) = cosx + isinx`, which is an identity used many, many times to solve the Schroedinger Equation in Physical Chemistry, by substituting `i` for various different constants.

---

What is accepted by Physical Chemists is that you can write out the general solution to the Equation as:

`y(x) = c_1 e^(alphax) + c_2 e^(-alphax)`

where `alpha = iomegat` and, after various proofs and empirical tests, it is agreed that we can use `e^(alphax)` as a working "trial function" when we guess the form of the overall solution in terms of a finite addition of these `c*e^(alphax)` functions so that we can predict molecular properties:

`psi(x) = sum_(i=1)^N c_i phi_i(x)`
where each `phi` could, for example, represent an atomic orbital, and `psi(x)` would in that case be the molecular orbital.

A common example of solving the time-dependent Schroedinger equation is (example 2-4 in Physical Chemistry: A Molecular Approach):

`(d^2x(t))/(dt^2) + omega^2x(t) = 0`

subject to the boundary conditions `x(0) = A` and `(dx(0))/(dt) = 0`. These boundary conditions define the fact that a stationary transverse wave with one antinode has two endpoints, and these are at `x = 0` and `x = l`, half of the wavelength.

To solve this one, one would have to use identity written at the top, with `alpha` substituted for `i` like so:

`c_1e^(alphax) + c_2e^(-alphax)`

`= c_1(cosx + alphasinx) + c_2(cosx - alphasinx)`

`= c_1cosx + c_1alphasinx + c_2cosx - c_2alphasinx`

`= (c_1 + c_2)cosx + (c_1alpha - c_2alpha)sinx`

and it is generally written out by absorbing the arbitrary constants `c_1`, `alpha`, and `c_2` into new arbitrary constants `c_3` and `c_4`, with `c_1 + c_2 = c_3` and `c_1alpha - c_2alpha = c_4`:

`= c_3cosx + c_4sinx`

Then, substituting `omegat` for `x`, we get:

`c_3cos(omegat) + c_4sin(omegat)`

for the solution to the so-called common example.

Looking at the boundary condition `(dx(0))/(dt) = 0`, we get:

`= c_3(-sin(omegat))*omega + c_4cos(omegat)*omega`

`= cancel(c_3(-sin(omega(0)))*omega)^(0) + c_4cos(omega(0))*omega`

`= c_4omega`

But we know that at `t = 0`, `omega = 0` because time has not passed yet.

`=> c_4omega = 0`, thus satisfying the condition `(dx(0))/(dt) = 0`.

Using the `x(0) = A` boundary condition we get:

`x(0) = c_3cos(omega(0)) + cancel(c_4sin(omega(0)))^(0)`

`= c_3`

with `c_3` taken as `A`---which is the amplitude of an initialized stationary wave---since it is the only contributor to the wave. Thus, since `c_3 = A`, we have satisfied the condition `x(0) = A`, and we just have:

`color(blue)(x(t) = Acos(wt))`

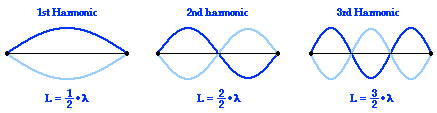
which is the familiar physics equation for a transverse wave, as depicted in the image above! :)