What volume flask should be used to get 0.37 moles #I# present for every mole #I_2# at equilibrium?
For the dissociation of #I_2"(g)"# at 1200°C, #K_c=0.011# . What volume flask should we use if we want 0.37 moles of #I# to be present for every mole of #I_2# present at equilibrium?
#I_2"(g)"\rightleftharpoons2I"(g)"#
My work:
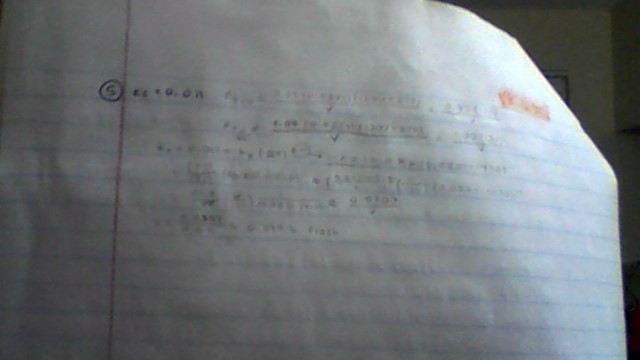
(can't see? it sets equilibrium pressures as stated below:)
#P_I=\frac{0.37*0.0821(1200+273)}{V}=\frac{0.37*121}{V}" atm"#
#P_(I_2)=\frac{1.00*0.0821(1200+273)}{V}=\frac{1.00*121}{V}=121/V" atm"#
after using those pressures for #K_p# in the formula #\color(red)(K_c=K_p(RT)^(\Deltan))# , I got #V=0.0307/0.011\approx0.279" L"#
For the dissociation of
My work:
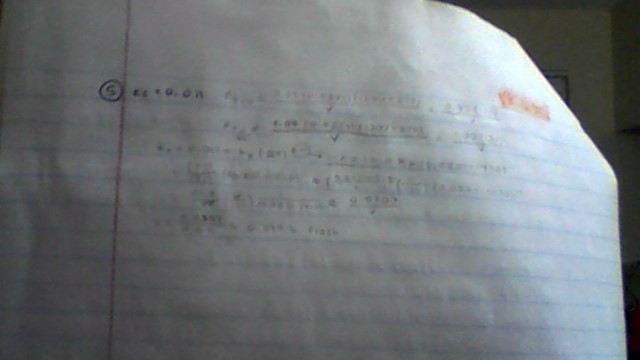
(can't see? it sets equilibrium pressures as stated below:)
after using those pressures for
1 Answer
Are we missing information? We need to be able to figure out the exact number of mols of
We begin with the ICE table:
#"I"_2(g) " "rightleftharpoons" " 2"I"(g)#
#"I"" "["I"_2]_i" "" "" "" "0#
#"C"" "-x" "" "" "+2x#
#"E"" "["I"_2]_i-x" "" "2x#
So we write the mass action expression to get:
#K_c = 0.011 = (["I"]^2)/(["I"_2])#
#= (2x)^2/(["I"_2]_i - x)#
What we apparently want is
#(2x)/(["I"_2]_i - x) = 0.37 = (["I"])/(["I"_2]) = ("mols I"//cancel"L")/("mols I"_2//cancel"L")#
We now have a system of equations:
#(2x)^2/(["I"_2]_i - x) = 0.011# #" "" "bb((1))#
(Note that#0.011# is in implied units of#"M"# .)
#(2x)/(["I"_2]_i - x) = 0.37# #" "" "bb((2))#
(Note that#0.37# is unitless.)
By inspection, we have:
#(2x)^2/(["I"_2]_i - x) = 0.011 = 0.37(2x) = 0.74x#
So,
#x = ("0.011 M")/0.74 = ul"0.0149 M"#
As a result, take
#(2 cdot "0.0149 M")/(["I"_2]_i - "0.0149 M") = 0.37#
#2 cdot "0.0149 M" = 0.37(["I"_2]_i - "0.0149 M")#
#"0.0297 M" = 0.37["I"_2]_i - "0.0055 M"#
Therefore, the initial concentration of
#color(blue)(["I"_2]_i) = ("0.0352 M")/(0.37) = color(blue)("0.0952 M")#
and the fraction of dissociation is
#alpha = x/(["I"_2]_i) = 0.1565#
Now we just need to know the ACTUAL mols of either
The fraction of dissociation

