What would the nuclear equation be for the beta-decay of strontium-90?
1 Answer
Here's what I got.
Explanation:
Strontium-90,
A beta particle,
At the same time, a
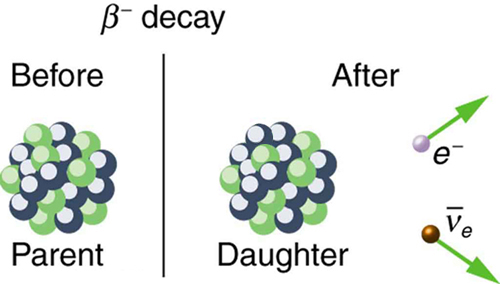
Now, because a neutron is being converted into a proton, the mass number of the nuclide will not change. However, its atomic number, which tells you how many protons are present inside the nuclues, will change.
More specifically, the atomic number will increase by
This means that the daughter nuclide will have an atomic number of
38 + 1 = 39
Another quick look in the periodic table will reveal that the daughter nuclide is yttrium-90,
You can thus write out the nuclear equation that describes the beta minus decay of strontium-90 like this
color(green)(|bar(ul(color(white)(a/a)color(black)(""_ 38^90"Sr" -> ""_ 39^90"Y" + ""_ (-1)^(color(white)(aa)0)beta + bar(nu)_"e")color(white)(a/a)|)))
Notice that mass and charge are conserved, since
overbrace(90 = 90 + 0)^(color(blue)("conservation of mass"))" " and" "overbrace(38 = 39 + (-1))^(color(darkgreen)("conservation of charge"))

