When 2 heterozygotes were crossed with each other i.e. AaBbAaBb x AaBbAaBb, the progeny showed: (i) A_B_ = 400 (ii) A_bb = 310 (iii) aaB_ = 290 (iv) aabb = 200 Does this prove Mendelian ratio? Find with a chi square test. (A and B- dominant)
1 Answer
The results of the dihybrid cross in question do not indicate Mendel's law of independent assortment.
Explanation:
The Mendelian ratio of a dihybrid cross is expected to create
To determine the expected numbers of genotypes in the progeny of the cross in question, multiply the number of each genotype times its expected ratio out of
The Chi-square
Genotype:
Observed:
Expected:
Genotype:
Observed:
Expected:
Genotype:
Observed:
Expected:
Genotype:
Observed:
Expected:
Determine the Chi-Square Sum
Once you have the Chi-Square sum, you need to use the Probability table below to determine the probability that the results of the dihybrid cross is due to the Mendelian inheritance of independent assortment.
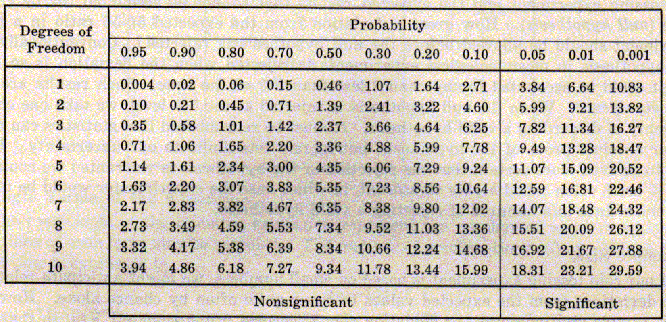 http://faculty.southwest.tn.edu/jiwilliams/probability.htm
http://faculty.southwest.tn.edu/jiwilliams/probability.htm
The degree of freedom is the number of categories in the problem minus 1. In this problem there are four categories, so the degree of freedom is 3.
Follow Row
The sum of

