When monochromatic light shines perpendicularly on a soap film (n= 1.35) with air on each side, the second smallest nonzero film thickness for which destructive interference of reflected light is observed is 296 nm . What is the wavelength of the light ?
2 Answers
film Thickness
Explanation:
Suppose monochromatic light is incident on a thin film of thickness
t and having an index of refraction n. Part of this light reflects back
toward the observer from the top and bottom surfaces of the thin
film toward the observer, and part is transmitted through the thin film.
the extra distance travelled by the ray which got reflected from
the bottom is twice the thickness of the thin film at the point
where the light is incident. This extra distance and the
corresponding phase differences of the two rays are related to each other as
phase difference/
here
path difference = 2.t. and
for destructive interference
for 2nd destructive interference m =1
2.t.n = (3/2).
therefore thickness
Explanation:
As the light enters the film of soap from air it partially reflects and refracts. The refracted ray continues travelling downward to the lower surface of the soap where it partially reflects and refracts. The reflected ray then moves upwards toward the upper surface of the soap. It then partially reflects and refracts again. The ray that refracts back into the air then overlaps with the ray that was initially reflected at the upper surface - both rays are moving upward - so they superpose.
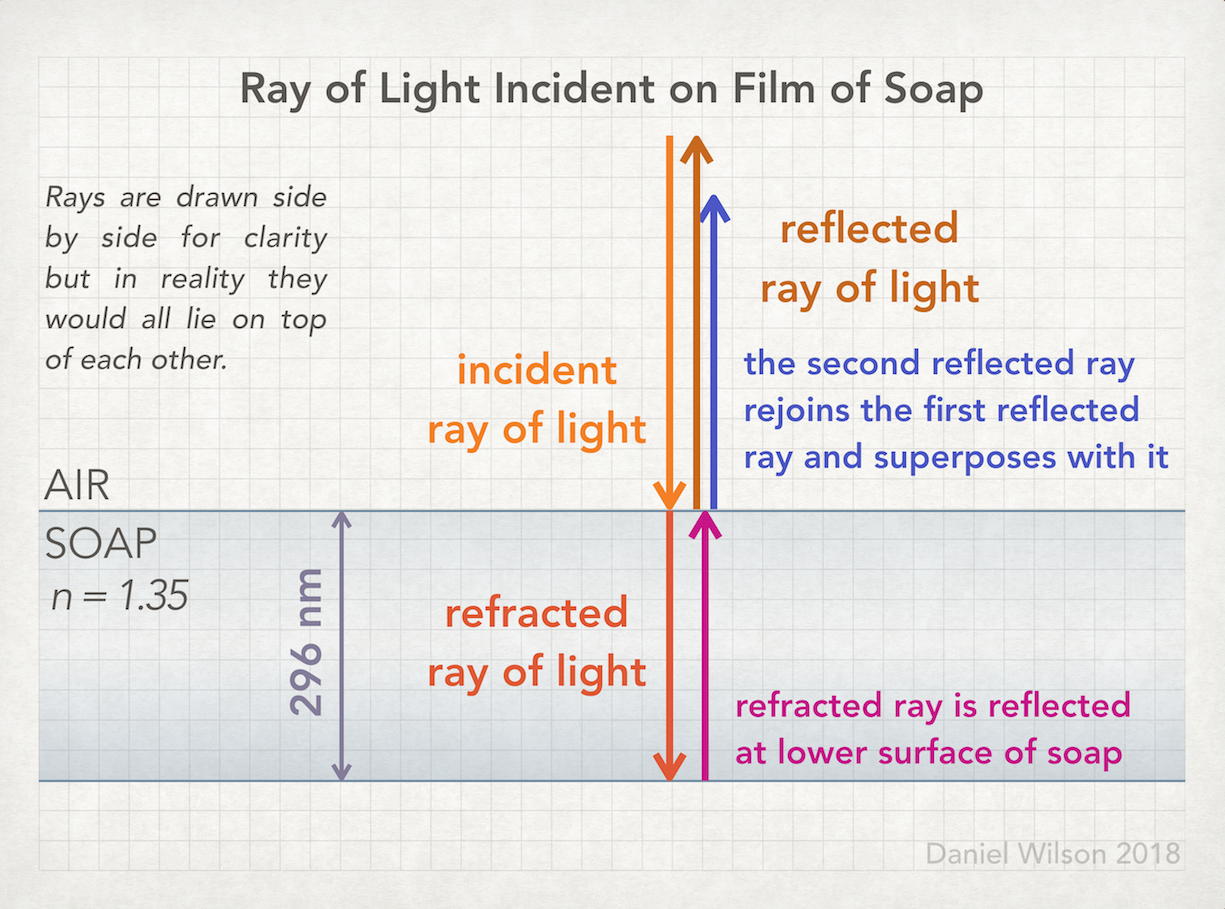
When the ray enters the soap film and refracts its wavelength gets shorter. When it re-emerges travelling upwards it refracts again but this time the wavelength increases back to its initial value in air.
The ray that was reflected at the lower surface of the film of soap travelled further than the ray reflected at the upper surface so there is a path difference (a difference in the distance travelled by the two rays). The path difference is equal to twice the thickness of the film of soap since the ray travels to the lower surface of the film and back in order to rejoin the first reflected ray.
Path Difference, ∆x
We are told in the question that the thickness of 296 nm is the second non-zero thickness of film that causes destructive interference. The relationship between path difference and wavelength for destructive interference is:
Where n is an integer.
The first destructive interference occurs when n = 0, the second occurs when n = 1. So the relationship then becomes:
Note that since the path difference occurs in the film we have just calculated the wavelength of the light in soap.
In order to calculate the wavelength of the light in air (which is what I think the question wants) we need to use the refractive index.
And
For this solution I will assume that the refractive index of air is 1.00 and that the speed of light in air is equal to the speed of light in a vacuum (variable c in the equation above). Remember that frequency is constant during refraction. So we can combine the above equations as follows:
Now substitute the value for the wavelength in soap and refractive index for soap and calculate the wavelength in air:
That means that the light is somewhere in the region of green in the visible spectrum.


