Interference
Key Questions
-
Constructive interference occurs when the waves are in phase, and destructive interference when they are half a cycle out of phase.

If we add these two waves together, point-by-point, we end up with a new wave that looks pretty much like the original waves but its amplitude is larger. This situation, where the resultant wave is bigger than either of the two original, is called constructive interference. The waves are adding together to form a bigger wave.
-
Answer:
This happens when two or more waves that are out of phase with a path difference of (n+ 0.5)λ, interfere.
Explanation:
For example:
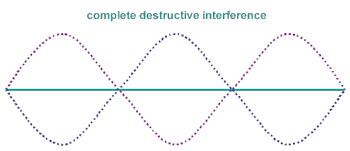
Here two coherent waves (in indigo and pink), are in antiphase (phase difference of 180 degrees), interfere destructively forming a resultant wave with with no displacement (application of principle of superposition). This will only occur if the interfering waves are of equal amplitudes and are out of phase.
Another example:
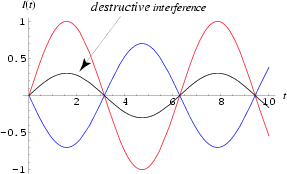
Here however, the waves are of different amplitudes and out of phase. By applying principle of superposition (1- 0.7 = 0.3 displacement units), the resultant wave has an amplitude less than that of any individual wave, but not zero as in the previous case.
Destructive interference can be observed as dark fringes (minimas) in case of light interference or flattened waves in case of water.
-
The amplitude is reduced to zero.
Destructive interference means that two identical waves (same amplitude and wavelength) arrive in anti phase. In that case wherever wave 1 is at a peak wave 2 will be at a trough and vice versa. The displacement of a trough is equal in magnitude to that of a peak but it is negative, so the sum of the displacements will be zero.