A conic equation of the type of #Ax^2+Bxy+Cy^2+Dx+Ey+F=0# is rotated by an angle #theta#, to form a new Cartesian plane with coordinates #(x',y')#, if #theta# is appropriately chosen, we can have a new equation without term #xy# i.e. of standard form.
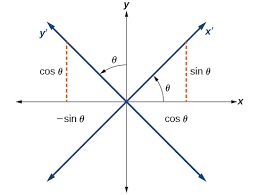
The relation between coordinates #(x,y)# and #(x'.y')# can be expressed as
#x=x'costheta-y'sintheta# and #y=x'sintheta+y'costheta#
or #x'=xcostheta+ysintheta# and #y=-xsintheta+ycostheta#
for this we need to have #theta# given by #cot2theta=(A-C)/B#
In the given case as equation is #3x^2+10xy+3y^2-9=0#, we have #A=3# and #B=10# and #C=3#, hence #cot2theta=0# i.e. #theta=pi/4#.
Hence, it is obvious that #xy# term is eliminated when rotateed through #pi/4# and the relation is give by #x=x'cos(pi/4)-y'sin(pi/4)# and #y=x'sin(pi/4)+y'cos(pi/4)# i.e.
#x=(x')/sqrt2-(y')/sqrt2# and #y=(x')/sqrt2+(y')/sqrt2#
Hence, we get #3((x')/sqrt2-(y')/sqrt2)^2+10((x')/sqrt2-(y')/sqrt2)((x')/sqrt2+(y')/sqrt2)+3((x')/sqrt2+(y')/sqrt2)^2-9=0#
or #3((x'^2)/2+(y'^2)/2-x'y')+10((x'^2)/2-(y'^2)/2)+3((x'^2)/2+(y'^2)/2+x'y')-9=0#
or #8x'^2-2y'^2-9=0#
The two graphs are as follows:
graph{3x^2+10xy+3y^2-9=0 [-10, 10, -5, 5]}
and
graph{8x^2-2y^2-9=0 [-10, 10, -5, 5]}

