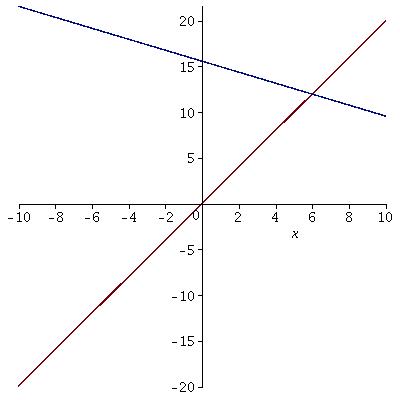
Where do the lines #3x+5y=78# and #2x-y=0# intersect?

Question

2976 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-09-13T22:10:19

lines intersect at #( 6 , 12 )#

If we equate one of the equations with the other, this will allow us to find a point or points that are common to both.

Rearrange both equations so they are in terms of y.

#y = 2x#

#y = -3/5x + 78/5#

This leads to:

#2x = -3/5x + 78/5#

Solving for #x#:

Multiplying both sides by #5#

#10x = -3x + 78#

Adding #3x# to both sides:

#13x = 78 => x = 6#

Plugging #6# into the equation #y = 2x#:

#y = 2(6) => y = 12#

So lines intersect at #( 6 , 12 )#

Graph:

enter image source here