Problem Solving with Linear Graphs
Key Questions
-
I assume that the equation you would be creating is in slope-intercept form, or
#y= mx + b# .If so, there is a simple answer. You can tell that you need to create a linear equation by the information the problem gives you. The problem should list the Y- intercept, a starting amount of something and a slope, or a rate of change.
For example, here is a problem:
Maddie and Cindy are starting their very own babysitting business. They charge parents $5 dollars right when they come in and $2 for every hour they need to babysit a child. How can they calculate how much they will charge for an evening of babysitting?
Your formula would be:
#y= 2x + 5# Your
#x# value would be hour(s) and your#y# value would be total cost. After you write your equation you can simply solve it. -
Lets take up a example
The admission fee at a small fair is $1.50 for children and $4.00 for adults. On a certain day, 2200 people enter the fair and $5050 is collected. How many children and how many adults attended?
number of adults: a
number of children: ctotal number:
#a + c = 2200 #
total income:#4a + 1.5c = 5050# here we are doing the basic declaration
#a = 2200 – c# #4(2200 – c) + 1.5c = 5050 # here we framing the equation to solve
#8800 – 4c + 1.5c = 5050 # #8800 – 2.5c = 5050 # #–2.5c = –3750 # #c = 1500#
finally we are numbers to get the final answer
#a = 2200 – (1500) = 700# There were 1500 children and 700 adults.
-
Here is a simple example of a word problem where graph helps.
From a point
#A# on a road at time#t=0# one car started a movement with a speed#s=U# measured in some units of length per unit of time (say, meters per second).Later on, at time
#t=T# (using the same time units as before, like seconds) another car started moving in the same direction along the same road with a speed#s=V# (measured in the same units, say, meters per second).At what time the second car catches on with the first, that is both will be on the same distance from point
#A# ?Solution
It makes sense to define a function that represents a dependency of the distance
#y# covered by each car from time#t# .The first car started at
#t=0# and moved with a constant speed#s=U# . Therefore, for this car the linear equation expressing this dependency looks like#y(t)=U*t# .The second car started later by
#T# units of time. So, for the first#T# units it covered no distance, so#y(t)=0# for#t<=T# . Then it starts moving with a speed#V# , so it's equation of movement will be#y(t)=V*(t-T)# for#t>T# . In this case a function is defined by two different formulas on two different segments of the argument#t# (time).Algebraically, the solution to this problem can be found by solving an equation
#U*t=V*(t-T)#
that results in
#t=(V*T)/(V-U)# Obviously,
#V# should be greater than#U# (otherwise, the second car would never catch up with the first).
Let's use concrete numbers:
#U=1#
#V=3#
#T=2#
Then the solution is:
#t=(3*2)/(3-1)=3# If we are not so well versed in Algebra and equations to construct the equation above, we can use graphs of these two functions to visualize the problem.
The graph of a function#y(t)=1*t# looks like this:
graph{x [-1, 10, -1, 10]}
The graph of a function#y(t)=0# if#t<=2# and#y(t)=3*(t-2)# if#t>2# looks like this:
graph{1.5x+|1.5x-3|-3 [-1, 10, -1, 10]}
If we draw both graphs on the same coordinate plane, the point they intersect (looks like#t=3# when both functions equal to#3# ) would be the time both cars are at the same location. This corresponds to our algebraic solution#t=3# .In this and many other cases the graph might not provide an exact solution, but it helps a lot to understand the reality behind a problem.
Moreover, graphical representation of a problem would help to find a precise analytical approach to exact solution. In the example above this process of intersecting two graphs gives a strong hint to an equation used to algebraically solve the problem. -
If you have a linear graph you can find corresponding values from one axis (or scale) to another.
This is most easily seen by an example:
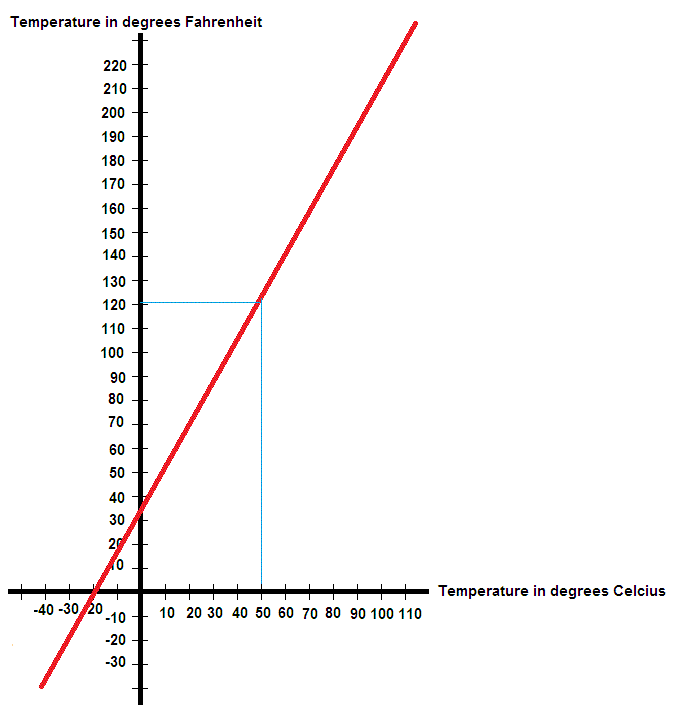
Here we have the linear graph showing the relationship between temperatures measured in Fahrenheit and in Celsius.
If you wanted to know what
#50^o# C was in the Fahrenheit scale, you would follow a vertical line up from the#50# on the Celsius axis, to the linear graph line, then move horizontally across to the Fahrenheit axis to get a reading of (approximately) a lit more than#120^o# F. (See the light blue lines for this procedure).If your problem was to convert a temperature in Fahrenheit to Celsius you would simply reverse the process ( horizontal across to the linear graph line from the Fahrenheit temperature and then horizontally down to the Celsius equivalent.
The accuracy of your result will of course depend upon how accurate your graph has been drawn.
Questions
Graphs of Linear Equations and Functions
-
Graphs in the Coordinate Plane
-
Graphs of Linear Equations
-
Horizontal and Vertical Line Graphs
-
Applications of Linear Graphs
-
Intercepts by Substitution
-
Intercepts and the Cover-Up Method
-
Slope
-
Rates of Change
-
Slope-Intercept Form
-
Graphs Using Slope-Intercept Form
-
Direct Variation
-
Applications Using Direct Variation
-
Function Notation and Linear Functions
-
Graphs of Linear Functions
-
Problem Solving with Linear Graphs