Question

Where is the vertex in the parabola y = x^2 +2x - 5? i dont understand this i need x and y intercepts and please show work?

Answer 1

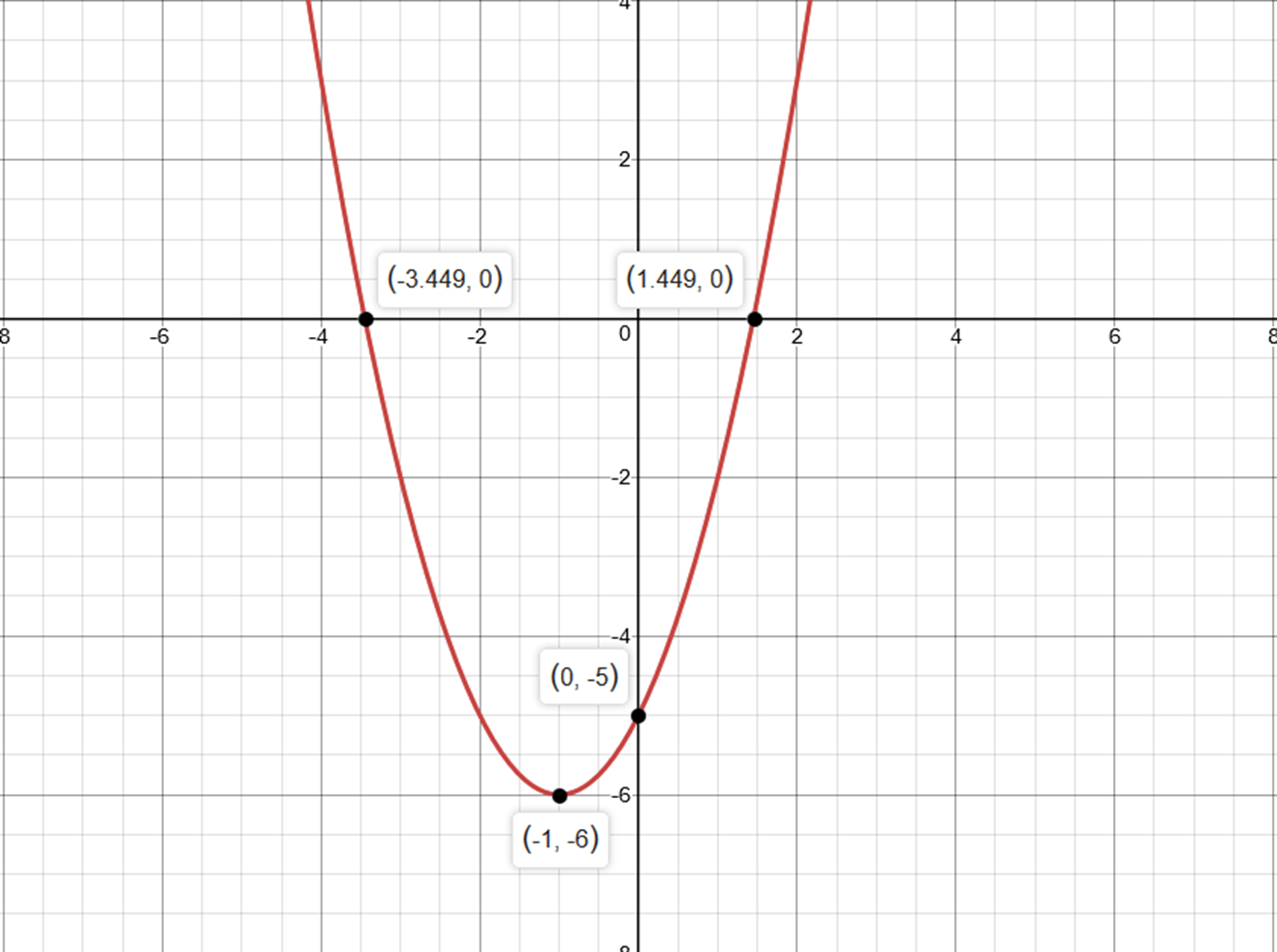
Vertex (-1, -6)

Explanation:

y = x^2 + 2x - 5
The x-coordinate of vertex is given by the formula:
x = - b/(2a) = - 2/2 = - 1
The y- coordinate of Vertex is given by y(-1), when x = -1 -->
y(-1) = (-1)^2 + 2(-1) - 5 = - 6
Vertex (-1, -6)
graph{x^2 + 2x - 5 [-20, 20, -10, 10]}

Answer 2

Vertex `(-1, -6)`
Y-intercept `(0,-5)`
x-intercept `(1.449, 0)`
x-intercept `(-3.449, 0)`

Explanation:

Given -

`y=x^2+2x-5`

Vertex is the point where the curve turns.
To find this point - first you have to calculate
for what value of `x` the curve turns. Use the formula to find that.

`x=(-b)/(2a)`

Where -
`b` is the coefficient of `x`
`a` is the coefficient of `x^2`

`x=(-2)/(2xx1)=(-2)/2=-1`

When `x` takes the value `-1` the curve turns. At that point `x` co ordinate is `-1`, then what is `y` coordinate. Plug in the `x=-1` in the given equation.

`y=(-1)^2+2(-1)-5=1-2-5=-6`

At point `(-1,-6)` the curve turns. This point is vertex.

Vertex `(-1, -6)`
Look at the graph.

What is `y` intercept?
It is the point at which the curve cuts the Y-axis. Look at the graph. At `(0, -5)` the curve cuts the Y-axis.
How to find it out?
Find the What is the value of `y` when `x` takes the value `0`

At `x=0; y=0^2+2(0)-5=0+0-5=-5`

At point `(0,-5)` the curve cuts the Y-axis.
Y-intercept `(0,-5)`

What is X-intercept?

It is the point at which the curve cuts the x-axis. Look at this graph. The curve cuts the x axis at two points. Then, how to find it out. Find the value(s) of `x` when `y=0`

`x^2+2x-5=0`
Solve to find the value of `x` [Squaring method is used]

`x^2+2x=5`
`x^2+2x+1=5+1=6`
`(x+1)^2=6`
`x+1=+-sqrt6=+-2.449`
`x=2.449-1=1.449`

x-intercept `(1.449, 0)`

`x=-2.449-1=-3.449`

x-intercept `(-3.449, 0)`