Question

Which element has a higher 3rd ionization energy, Al or Mg? Why?

Answer 1

Magnesium.

Explanation:

A quick look in the periodic table will reveal that aluminium, `"Al"`, and magnesium, `"Mg"`, are both located in period 3.

Now, assuming that you're not familiar with the periodic trends in ionization energy, you can determine which element will have a higher third ionization energy by taking a look at their respective electron configurations.

`"Mg: " 1s^2 2s^2 2p^6 3s^2" "` and `" " "Al: " 1s^2 2s^2 2p^6 3s^2 3p^1`

Check out this great diagram showing the two electron configurations side by side

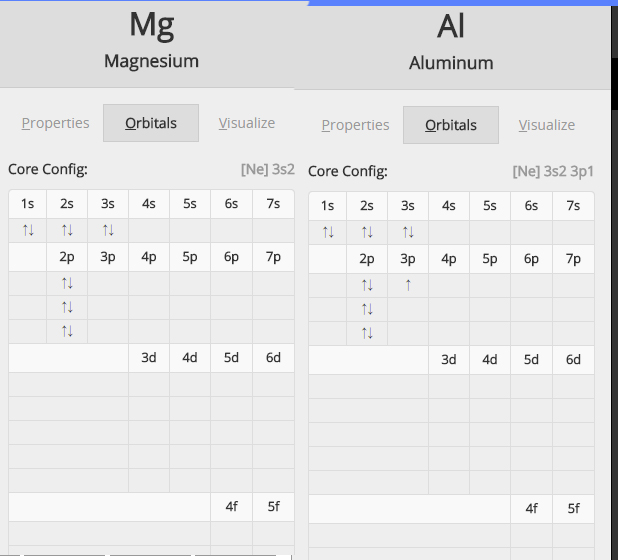
As you know, ionization energy is defined as the energy needed to remove one mole of electrons from one mole of atoms in the gaseous state

`X_((g)) + color(blue)("energy") -> X_((g))^(+) + e^(-)`

Now, the important thing to notice here is that magnesium has two electrons on its outermost energy level, both located in the 3s-orbital.

On the other hand, aluminium has three electrons located on its outermost energy level, one located in a 3p-orbital and two in the 3s-orbital.

The third ionization energy is the energy needed to remove a third electron from an atom.

`X_((g))^(2+) + color(blue)(3^"rd" "ionization energy") -> X_((g))^(3+) + e^(-)`

Notice that in aluminium's case, the third electron you would remove comes from the third energy level, more specifically from the 3s-orbital.

In magnesium's case, however, the third electron would come from the second energy level, more specifically from a 2p-orbital.

Since this third electron is located closer to the nucleus for magnesium than for aluminium, you can expect the third ionization energy to be higher in magnesium's case.

Not only is the third electron closer to the nucleus in magnesium's case, but it is screened les efficiently by the other electrons, including by the core electrons.

Both these factors contribute to the fact that the nucleus has a stronger grip on this electron, and hence more energy is needed to remove it.

Answer 2

Magnesium!

---

There is also an alternative way to approach this that is a bit different but builds on core principles you've been taught in General Chemistry, and distinguishes between the magnitude of increase in ionization energy:

• according to when one examines the `Z_(eff)`
• according to when one goes against the octet rule.

As stefan mentions, knowing the electron configurations is a great idea for this question; it helps accompany how you visualize the electron distributions.

THIRD IONIZATION ENERGY

Just as the first ionization energy involves removing the first electron from the highest energy orbital, the third ionization energy involves removing a third electron from the highest energy orbital.

How might one express this? Well, if we let more "`Delta`" mean the application of heat and `M` be a general metal:

`M(g) + Delta -> cancel(M^(+)(g)) + e^(-)`
`cancel(M^(+)(g)) + Delta -> cancel(M^(2+)(g)) + e^(-)`
`cancel(M^(2+)(g)) + Delta -> M^(3+)(g) + e^(-)`
`"---------------------------------"`
`M(g) + Delta -> M^(3+)(g) + 3e^(-)`

The question is, which element is less likely to be dandy with losing an electron?

ELECTRON CONFIGURATIONS & OCTETS

If you write out the electron configurations, note that `Mg` and `Al` are adjacent on the third period/row, and so the answer would have something to do with either the `Z_(eff)` or a more substantial effect. Let's see...

`Mg`: `1s^2 2s^2 2p^6 3s^2`
`Al`: `1s^2 2s^2 2p^6 3s^2 3p^1`

or...

`Mg`: `[Ne] 3s^2`
`Al`: `[Ne] 3s^2 3p^1`

Well, if we remove THREE electrons from each of these metals...

...what we end up doing after removing the third electron is turning `Al` into a `Ne`-like cation. That's pretty favorable, because it gives the atom an octet, which you've been taught is in line with stability and fairly inert qualities. That's why the common oxidation state for `Al` is `Al^(3+)`.

However, with `Mg`, what you end up doing is trying to remove the third electron from `Mg^(2+)`, which is already `\mathbf(Ne)` -like. That disrupts the stable octet it already has, and is unfavorable.

Hence, we would expect a drastic increase in the third ionization energy of `\mathbf(Mg)` compared to that of `\mathbf(Al)`, and there is!

`"IE"_(Mg)^((2)) = "1450.6 kJ/mol"`
`"IE"_(Mg)^((3)) = color(blue)("7732.6 kJ/mol")`

`"IE"_(Al)^((2)) = "1816.6 kJ/mol"`
`"IE"_(Al)^((3)) = color(blue)("2744.7 kJ/mol")`