Which equation best represents the line perpendicular to 2y=7x if the y-intercept is b=5?
3 Answers
Explanation:
The slope is
Explanation:
First find the slope of the given line which is
solve for
here the coefficient of x is the slope
the slope is =
now the line that we need to find is perpendicular so its slope is
the reciprocal of
the equation of the line that is perpendicular to
+5 because is given in the question that it will intersect y-axis at 5
you can check you equation by graphing them using graph calculators like
https://www.desmos.com/calculator
Desmos is a great calculator to graph equations and functions
The line perpendicular to
Explanation:
We should know that if you have a line
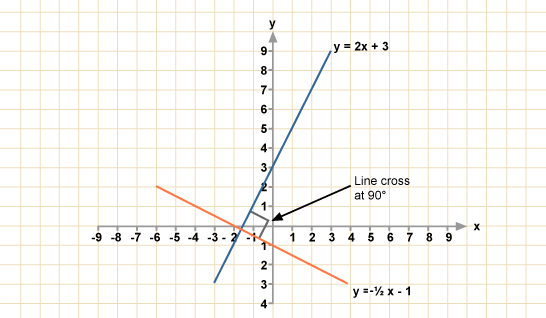
As this is a well known fact, I will take it as given. (See for instance http://www.bbc.co.uk/schools/gcsebitesize/maths/algebra/graphshirev1.shtml or http://www.coolmath.com/algebra/08-lines/14-perpendicular-lines-01
So let's write our line on the above form:
This means
Graphically we get:

