Which of the following is not a valid set of four quantum numbers? How can you determine this?
a. 2,0,0, + 1/2
b. 2,1,0, -1/2
c. 3,1, -1, -1/2
d. 1,0,0, +1/2
e. 1,1,0, +1/2?
a. 2,0,0, + 1/2
b. 2,1,0, -1/2
c. 3,1, -1, -1/2
d. 1,0,0, +1/2
e. 1,1,0, +1/2?
1 Answer
The answer is
Explanation:
Start by making sure that you're familiar with the valid values each quantum number can take.
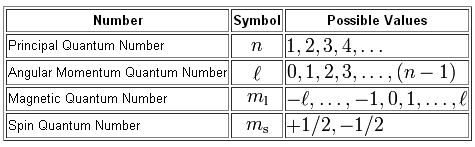
As you can see, the principal quantum number,
The spin quantum number is independent of the of the values taken by the other three quantum numbers and can only have two possible values,
Now, take a look at the relationship between the value of
This set is valid because
This quantum number set represents an electron located on the second energy level, in the s-subshell, in the
This set is valid because
#l = 0, 1, ..., (n-1)#
when
Once again, you're dealing with a valid set. All the quantum numbers are well within their accepted values. Notice that when
#m_l = {-1, color(white)(-)0, +1}#
This set represents an electron located on the third energy level, in the p-subshell, in the
This set is valid and it represents an electron located on the first energy level, in the s-subshell, in the
This is not a valid set of quantum numbers. Notice that
#n=1" "# and#" "l=1#
This means that the set cannot describe an electron located in an atom, i.e. it's not a valid set.

