Question

Which of the following sets of quantum numbers are not permitted?

`1: " "2, 1, 1, -1/2`

`2: " "2, 2, 1, +1/2`

`3: " "3, 2, 0, -1/2`

`4: " "4, 3, 2, -1/2`

`5: " "4,2,-3,+1/2`

Answer 1

Here's what I got.

Explanation:

As you know, the four quantum numbers that we use to describe the location and the spin of an electron in an atom are related as follows:

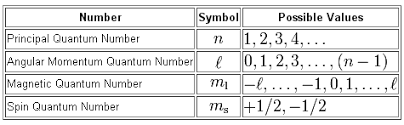
So all you have to do here is to look at which values are permitted for the four quantum numbers given to you for each set.

`n = 2, l = 1, m_l = 1, m_s = -1/2" " " "color(darkgreen)(sqrt())`

This is a valid set because all four quantum numbers have permitted values. In fact, this quantum number set describes an electron located in the second energy shell, in the `2p` subshell, in one of the three `2p` orbitals, that has spin-down.

`color(white)(a)`

`n = 2, l = 2, m_l = 1, m_s = +1/2" " " "color(red)(xx)`

This is not a valid set because the value of the angular momentum quantum number, `l`, cannot be equal to the value of the principal quantum number, `n`.

`n = 2 => l = {0, 1, color(red)(cancel(color(black)(2)))}`

`color(white)(a)`

`n = 3, l = 2, m_l = 0, m_s = -1/2" " " "color(darkgreen)(sqrt())`

This is a valid set because all four quantum numbers have permitted values. This quantum number set describes an electron located in the third energy shell, in the `3d` subshell, in one of the five `3d` orbitals, that has spin-down.

`color(white)(a)`

At this point, you should be able to look at the last two sets and say whether or not they can describe an electron in an atom, so I'll leave them to you as practice.