Question

Why are standard candles important to astronomers trying to measure the Hubble constant?

Answer 1

When Edwin Hubble first proposed his idea of universal expansion, it was based on the observation that the farther a galaxy was from the Earth, the faster it was moving away from us. When Hubble plotted the distances, `d`, to galaxies against the rate at which they were receding, `v`, he noticed that the plot followed a linear trend.

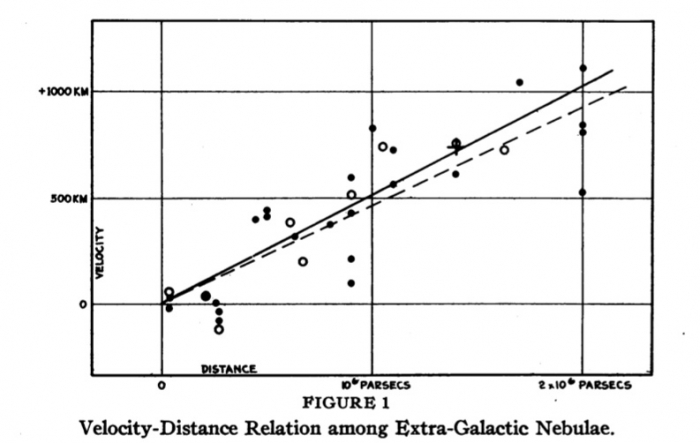
In other words the velocity at which galaxies are receding from us increases with distance at a constant rate. We can express this mathematically as;

`H_o = v/d`

Where `H_o` is the Hubble constant. In order to accurately calculate `H_o`, we need to know both the velocity and distance of the galaxies in question. The velocity can be found by measuring red shift. Check here for an explanation of how red shift works. Finding the distance to galaxies is more complicated, though. Parallax works pretty well for nearby stars, but galaxies are way too far to use parallax. That's where standard candles come in.

A standard candle is a light source for which we know the absolute magnitude. By comparing the absolute magnitude, `M_v`, to the apparent magnitude, `m`, we can find the distance to the candle. This relation, derived Here is given as;

`d=(10"pc")xx10^((m-M_v)/5)`

Hubble used Cepheid variable stars for his standard candle. Cepheid variables are stars that change their brightness over regular time intervals. This period of brightening and dimming is directly correlated with the absolute magnitude of the star.

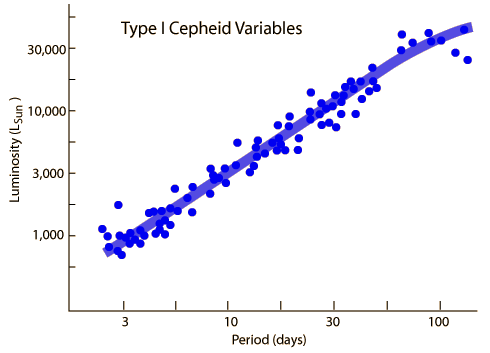
Cepheid variables are also incredibly bright, making them observable in other galaxies.