Why are the tangents for 90 and 270 degrees undefined?
2 Answers
This is a good question indeed!
Explanation:
I'll try to give you a visual explanation.
Consider the trigonometric meaning of tangent of an angle
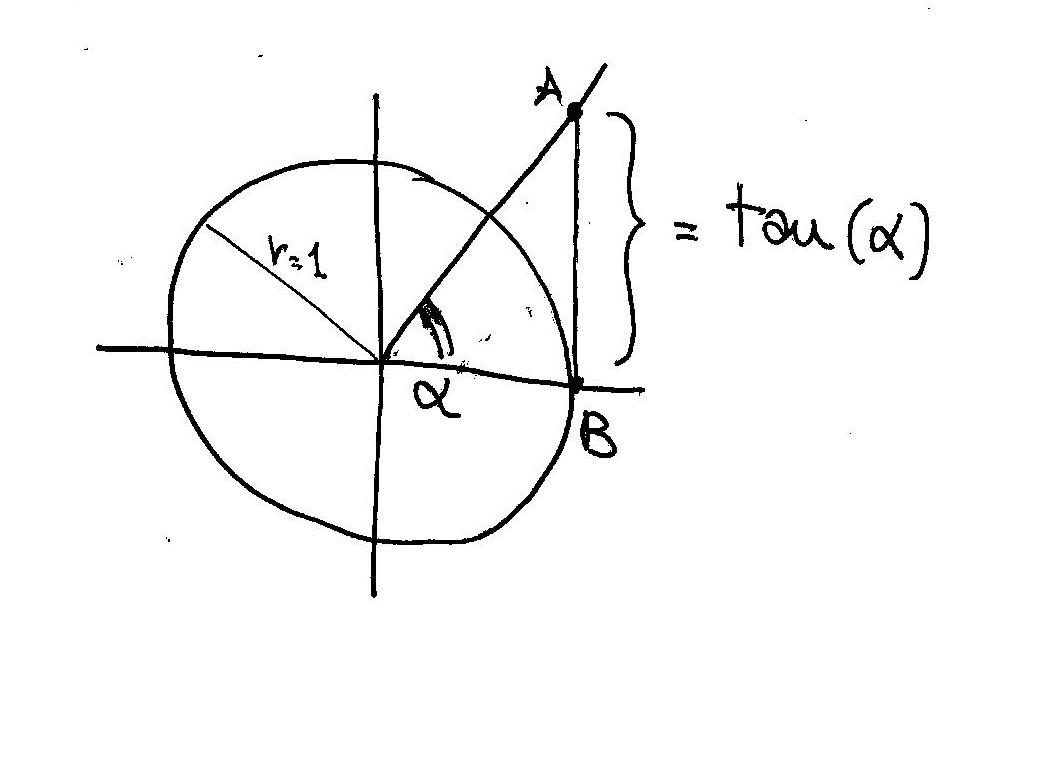
The tangent of
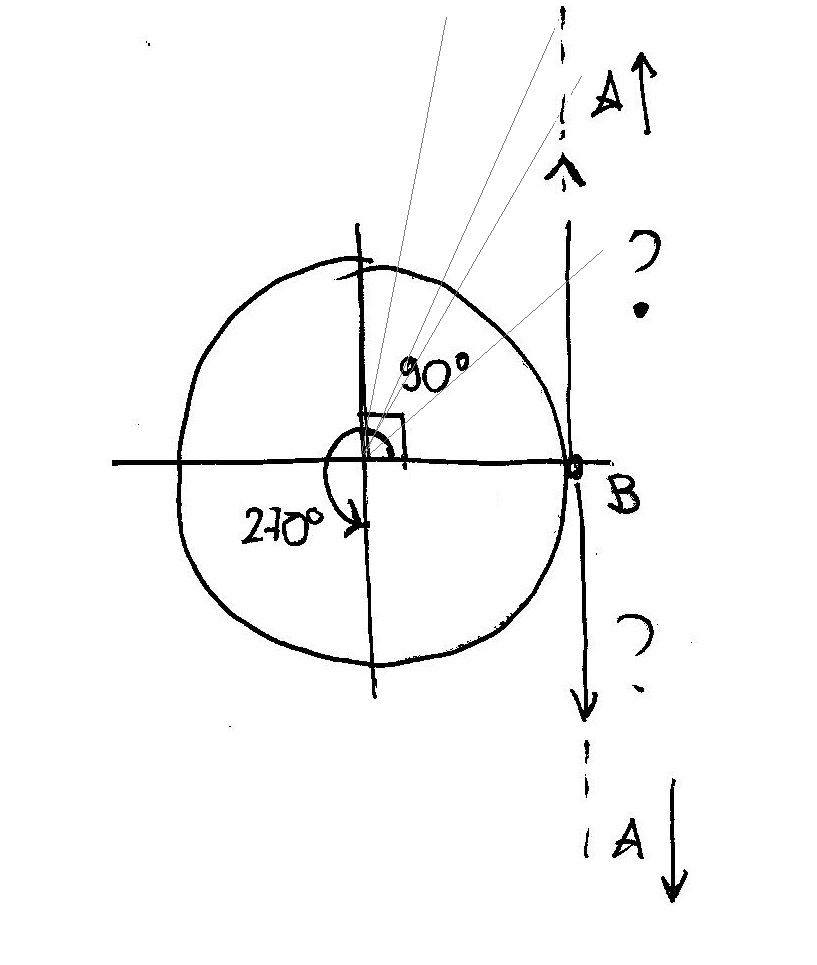
Hope it helps!
You can also say that
You can take a look at the overlap of
graph{(y - sinx)(y - cosx) = 0 [-0.034, 6.2831, -1.2, 1.2]}
We can establish that:
because
because both
We can also see that:
because
because both
Since the limits from the left and right side are not the same,


