Question

Why does `cos(90 - x) = sin(x)` and `sin(90 - x) = cos(x)`?

Answer 1

Note that the image below is only for `x` in Q1 (the first quadrant).
If you wish you should be able to draw it with `x` in any quadrant.

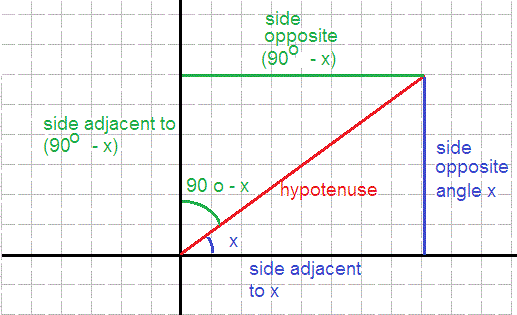
Definition of `sin(x)`

`(`side opposite angle `x)//(`hypotenuse`)`

Definition of `cos(90^@ -x)`

`(`side adjacent to angle `(90^@-x))//(`hypotenuse`)`

but `(`side opposite angle `x) = (`side adjacent to angle `(90^@-x)`

Therefore

`sin(x) = cos(90^@ -x)`

Similarly

`cos(x) = sin(90^@ - x)`

Answer 2

These can also be proven using the sine and cosine angle subtraction formulas:

`cos(alpha-beta)=cos(alpha)cos(beta)+sin(alpha)sin(beta)`

`sin(alpha-beta)=sin(alpha)cos(beta)-cos(alpha)sin(beta)`

Applying the former equation to `cos(90^@-x)`, we see that

`cos(90^@-x)=cos(90^@)cos(x)+sin(90^@)sin(x)`

`cos(90^@-x)=0*cos(x)+1*sin(x)`

`cos(90^@-x)=sin(x)`

Applying the latter to `sin(90^@-x)`, we can also prove that

`sin(90^@-x)=sin(90^@)cos(x)-cos(90^@)sin(x)`

`sin(90^@-x)=1*cos(x)-0*sin(x)`

`sin(90^@-x)=cos(x)`