Question

Why does the vertical line test work?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`
Let us say we have a graph drawn for a mathematical relation.

`color(red)(y=f(x)=x^2`

This is a mathematical relation, as for every value of `color(blue)(x`, there is a corresponding value of `color(blue)(y`.

To check whether this graph is a function, a Vertical Line Test can be used.

Let us examine the following graph drawn for the mathematical relation:

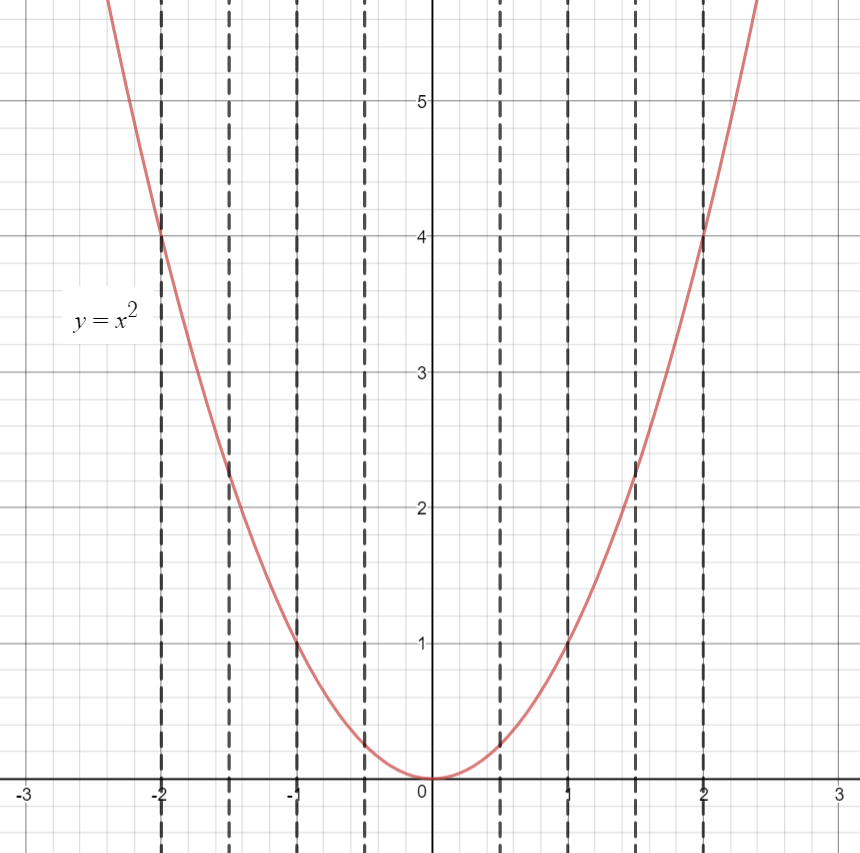
Can you observe the vertical lines drawn for various values of `color(red)(x` ?

All of these vertical lines intersect the graph at one point only.

If there is just one point of intersection,

that would mean,

for every x-value, there is just one unique y-value.

This property proves that the given mathematical relation

`color(red)(y=f(x)=x^2`

is a mathematical function.

Hence, the vertical line test works in determining whether a given relation is a function.

Let us try one more mathematical relation:

`color(blue)(y^2=-4x`

This mathematical relation creates a parabola and the parabola is symmetric about the x-axis, at `color(red)(y=0`.

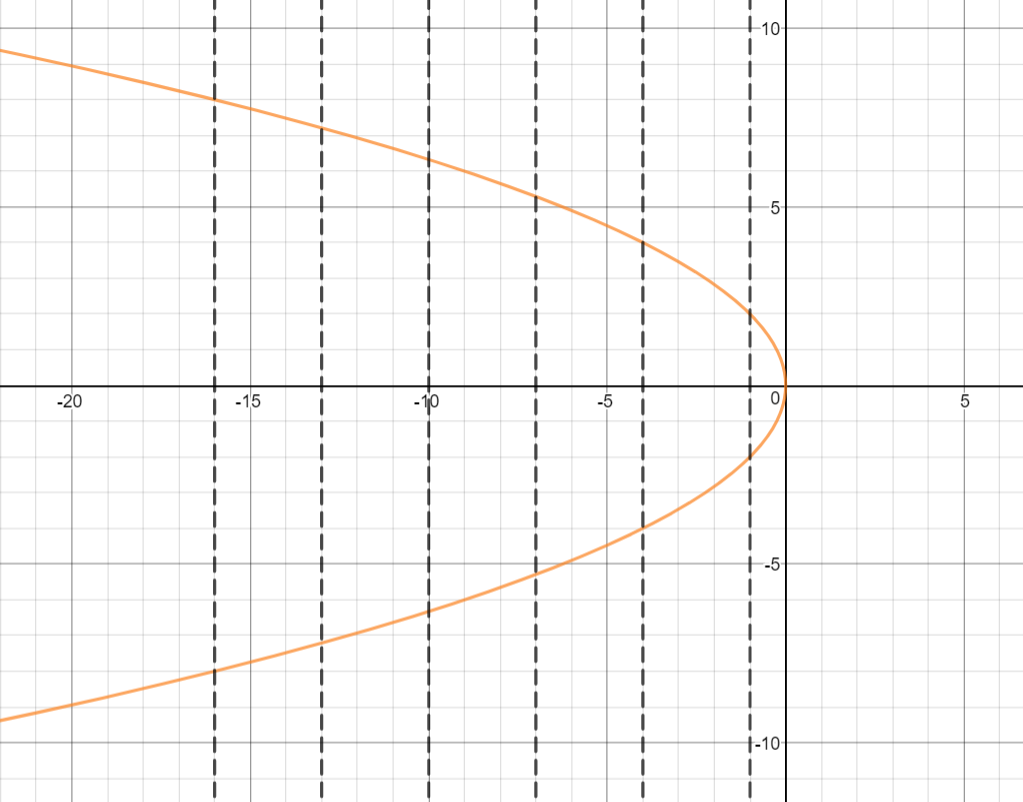
This mathematical relation

`color(blue)(y^2=(-4x)` is NOT a function,

as the vertical line test fails.

Hope it helps.