Question

Why is the phase diagram of water so odd?

Answer 1

Because the slope of the liquid-solid coexistence curve (the line `bar(DA)`) is negative, implying that water expands when it freezes, instead of contracting like many other substances do.

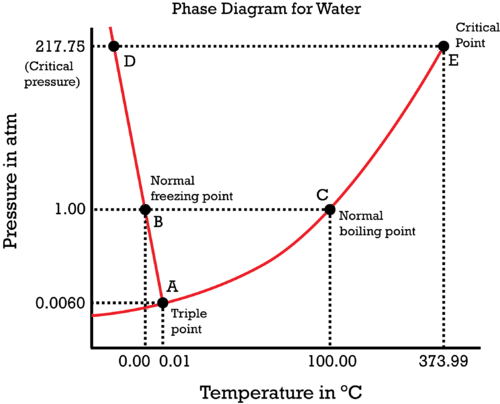
To rationalize this, we turn to the Clapeyron equation.

`(dP)/(dT) = (Delta_fbarH_A)/(T_(f)DeltabarV_A^((s) -> (l)))`

This equation describes the slope of the liquid-solid coexistence curve. Now, since:

• this slope, `(dP)/(dT)`, is known to be negative,
• temperature in `"K"` is always positive,
• and the `Delta_fH` (enthalpy of fusion) for melting is positive,

the change in molar volume for a melting solvent, `bb(DeltabarV_A^((s)->(l)))` , must be negative. That means water contracts when it melts and expands when it freezes, unlike many other liquids.

See below if you want to see how one can derive this equation.

---

DISCLAIMER: This is a derivation. If you have to know it, or if you're curious, read on.

At the liquid-solid coexistence curve, the chemical potential, `mu` (equal to `G/n`, the molar Gibbs' free energy), of the solvent `A`, on either side, is equal:

`mu_A^((s)) = mu_A^((l))`

Chemical potential is basically the tendency to move towards a certain energetic direction.

Since these chemical potentials are equal, there is no tendency to stay in one particular phase over the other, so the infinitesimally small change in chemical potential for melting is `0`:

`dmu_A^((s) -> (l)) ~~ Deltamu_A^((s) -> (l)) = mu_A^((s)) - mu_A^((l)) = 0`

Now, note that `mu = G/n`, the molar Gibbs' free energy, and that the Maxwell Relation for `G` is:

`dG = -SdT + VdP`

where `S` is entropy and the remaining variables (`T,P`) are well-known.

Similarly, if we let `G/n = barG`, then:

`dDeltamu_A = dDeltabarG_A = -DeltabarS_AdT + DeltabarV_AdP`

Now, if we set `dDeltamu_A = dDeltamu_A^((s) -> (l)) = 0` at this phase boundary, then:

`0 = -Delta_fbarS_AdT + DeltabarV_A^((s) -> (l))dP`

`Delta_fbarS_AdT = DeltabarV_A^((s) -> (l))dP`

`(Delta_fbarS_A)/(DeltabarV_A^((s) -> (l)))dT = dP`

This gives us the Clapeyron equation:

`color(green)((dP)/(dT) = (Delta_fbarS_A)/(DeltabarV_A^((s) -> (l))))`

where `Delta_fbarS` is the molar enthalpy of fusion. Or, if we recognize that `DeltaG = 0` at a phase equilibrium, then `Delta_fS = (Delta_fH)/T`, and we have an easier version to interpret:

`color(blue)((dP)/(dT) = (Delta_fbarH_A)/(T_(f)DeltabarV_A^((s) -> (l))))`

where `T_f` is the freezing point.

This equation describes the slope of the liquid-solid coexistence curve.