Why is the unit circle and the trig functions defined on it useful, even when the hypotenuses of triangles in the problem are not 1?
1 Answer
Trig functions tell us the relationship between angles and side lengths in right triangles. The reason that they are useful has to do with the properties of similar triangles.
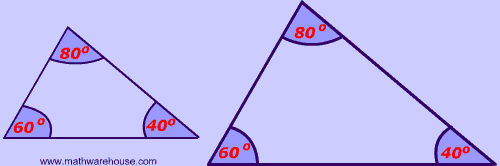
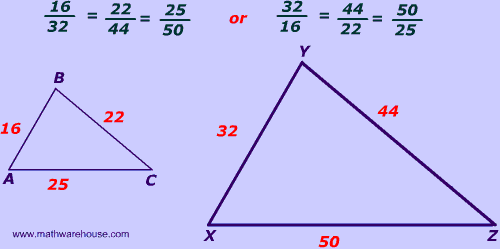
Similar triangles are triangles that have the same angle measures. As a result, the ratios between similar sides of two triangles are the same for each side. In the image below, that ratio is
The unit circle gives us relationships between the lengths of the sides of different right triangles and their angles. All of these triangles have a hypotenuse of
 )
)
Lets suppose we have a
So to solve the other sides of the triangle, we just need to multiply
 )
)
You can solve any right triangle that you know at least one side of by finding a similar triangle on the unit circle, then multiplying

