Applying Trig Functions to Angles of Rotation
Key Questions
-
1st and 3rd quadrants. You can use the CAST diagram which tells you in which quadrants angles are positive. ie. cos (and its reciprocal sec) is + in the4th quad, All of them + in 1st quad, sin (and its reciprocal cosec) + in 2nd and tan and cot + in 3rd.
-
Answer:
See description below.
Explanation:
In mathematics, a unit circle is a circle with a radius of one. In trigonometry, the unit circle is the circle of radius one centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane.
The point of the unit circle is that it makes other parts of the mathematics easier and neater. For instance, in the unit circle, for any angle θ, the trig values for sine and cosine are clearly nothing more than sin(θ) = y and cos(θ) = x. ... Certain angles have "nice" trig values.
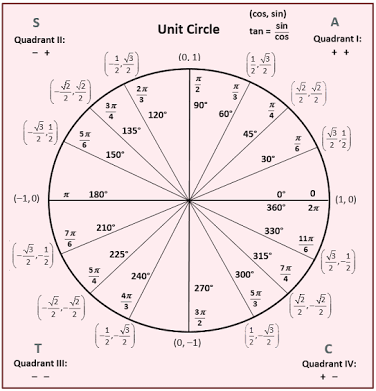
The circumfrence of the unit circle is
#2pi# . An arc of the unit circle has the same length as the measure of the central angle that intercepts that arc. Also, because the radius of the unit circle is one, the trigonometric functions sine and cosine have special relevance for the unit circle. -
Any angle of rotation
#theta# can be represented by a point#A# on a unit circle with a center at the origin of coordinates#O# and radius#1# . The angle is measured counterclockwise from the positive direction of the X-axis to a line from#O# to#A# , so#angle XOA=theta# with#|OA|=1# . Thus, an angle of#90^0# is represented by a point with coordinates#(0,1)# , an angle of#270^0# is represented by a point#(0,-1)# etc.Then, by definition, if point
#A# has coordinates#(A_x,A_y)# ,
#sin(theta)=A_y#
#cos(theta)=A_x#
#tan(theta)=A_y/A_x# (for#A_x!=0# )
#sec(theta)=1/A_x# (for#A_x!=0# )
#csc(theta)=1/A_y# (for#A_y!=0# )The above are definitions of trigonometric functions for any angles. The typical geometric definition of trigonometric functions using the right triangles is not general enough, while the above definitions work for all angles and, in case of acute angles in the right triangles, are identical to geometric definition.
I might suggest to study trigonometry at Unizor - Trigonometry. The site has a very detailed explanation of properties of trigonometric functions based on the above definition.