Families of Lines
Key Questions
-
A family of lines is a set of lines that have something in common with each other.
In brief, we can have two types of families of lines:
-
one where the slope is the same
#-># keep the slope unchanged and vary the#y# -intercept#-># parallel lines
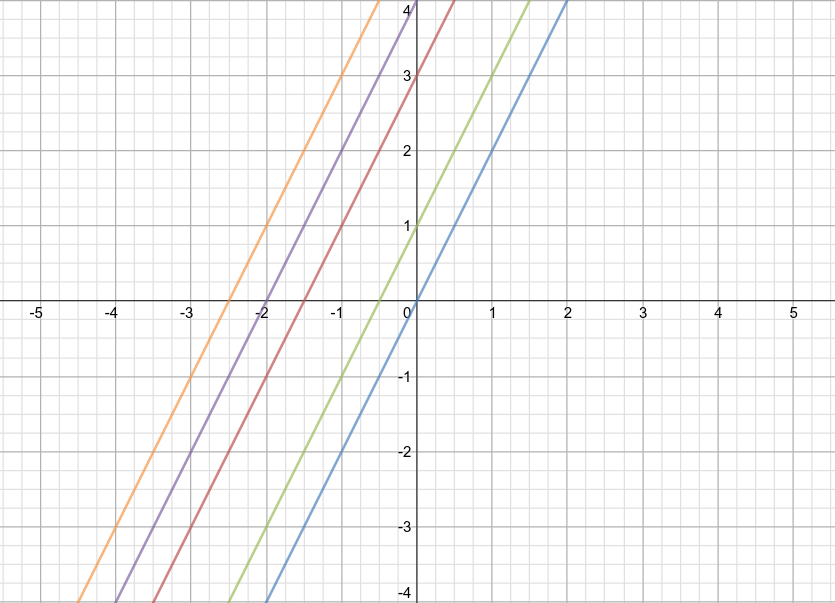
-
one where the
#y# -intercept is the same#-># keep the#y# -intercept unchanged and vary the slope#-># concurrent lines
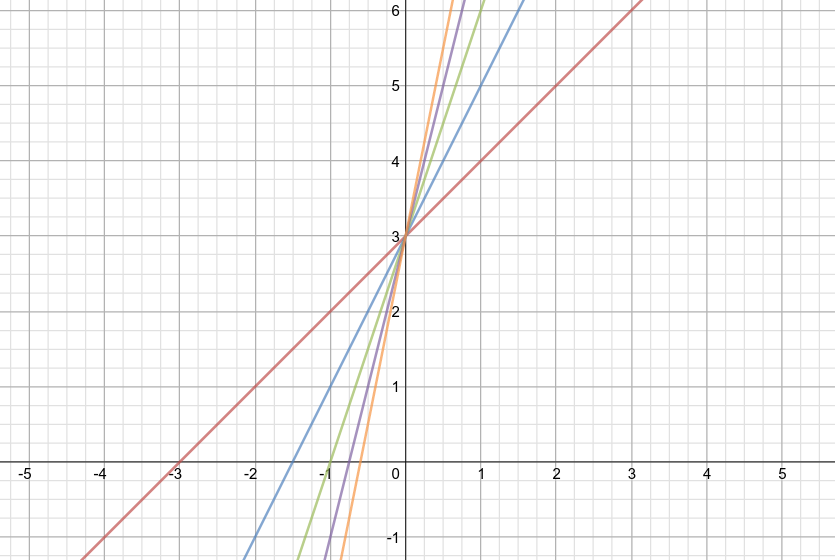
-
-
All lines following a specific criteria are called a family of lines.
For eg.
If the criteria is passing through a point (0,0)
Then all possible lines passing through that point are called the family of lines.If the criteria is have a slope of -1,
Then all possible lines have slope = -1 are its family of lines.
The idea is similar to human families where all our relatives belong to the same family (the criteria) and therefore everyone is a family member.
I hope this helps.
Questions
Forms of Linear Equations
-
Write an Equation Given the Slope and a Point
-
Write an Equation Given Two Points
-
Write a Function in Slope-Intercept Form
-
Linear Equations in Point-Slope Form
-
Forms of Linear Equations
-
Applications Using Linear Models
-
Equations of Parallel Lines
-
Equations of Perpendicular Lines
-
Families of Lines
-
Fitting Lines to Data
-
Linear Interpolation and Extrapolation
-
Problem Solving with Linear Models
-
Dimensional Analysis