Question

How do you use polar coordinates to evaluate the integral which gives the area that lies in the first quadrant between the circles `x^2+y^2=36` and `x^2-6x+y^2=0`?

Answer 1

Hello !

Do you really need integrals to calculate these aera ? Maybe I did not understand your problem, but the aera is easy :

`\mathcal{A} = \frac{1}{4}\pi\cdot 6^2 - \frac{1}{2}\pi\cdot 3^2 = \frac{9}{2}\pi`.

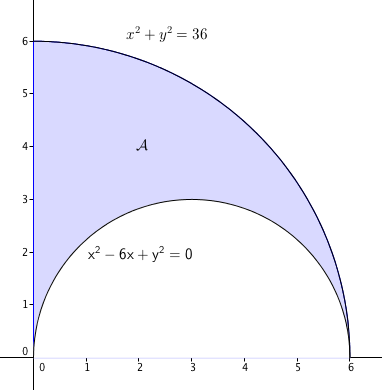
Explanations.

1) The area of a circle of radius `R` is `\pi R^2`.

Here you have to calculate area of `1/4` of circle of radius 6 (so, `\frac{1}{4}\pi\cdot 6^2`) and area of half circle of radius 3 (so, \frac{1}{2}\pi\cdot 3^2).

2) The equation `x^2+y^2=36` represents the circle of radius `\sqrt{36} = 6` and center `O(0,0)`.

The equation `x^2-6x+y^2=0` is too `(x-3)^2+ y^2=9`, therefore it represents the circle of radius `\sqrt{9}=3` and center `I(3,0)`.

Remark. `(x-a)^2 + (y-b)^2 = r^2` (with `r>0`) represents the circle of radius `r` and center `I(a,b)`.