Question

What is the length of the shortest ladder that will reach from the ground over the fence to the wall of the building if an 8ft fence runs parallel to a tall building at the distance of 4ft from the building?

Answer 1

Warning: Your math teacher will not like this method of solution!
(but it's closer to how it would be done in the real world).

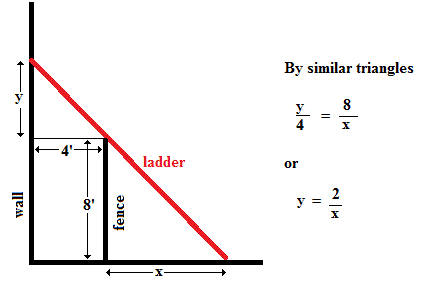
Note that if `x` is very small (so the ladder is almost vertical)
the length of the ladder will be almost `oo`
and if `x` is very large (so the ladder is almost horizontal)
the length of the ladder will (again) be almost `oo`

If we start with a very small value for `x` and gradually increase it
the length of the ladder will (initially) become shorter
but at some point it will need to start increasing again.

We can therefore find bracketing values a "low X" and a "high X" between which the ladder length will reach a minimum.

If this range is too large we can subdivide it to find a "midpoint" length and adjust our bracketing values to any reasonable degree of accuracy.

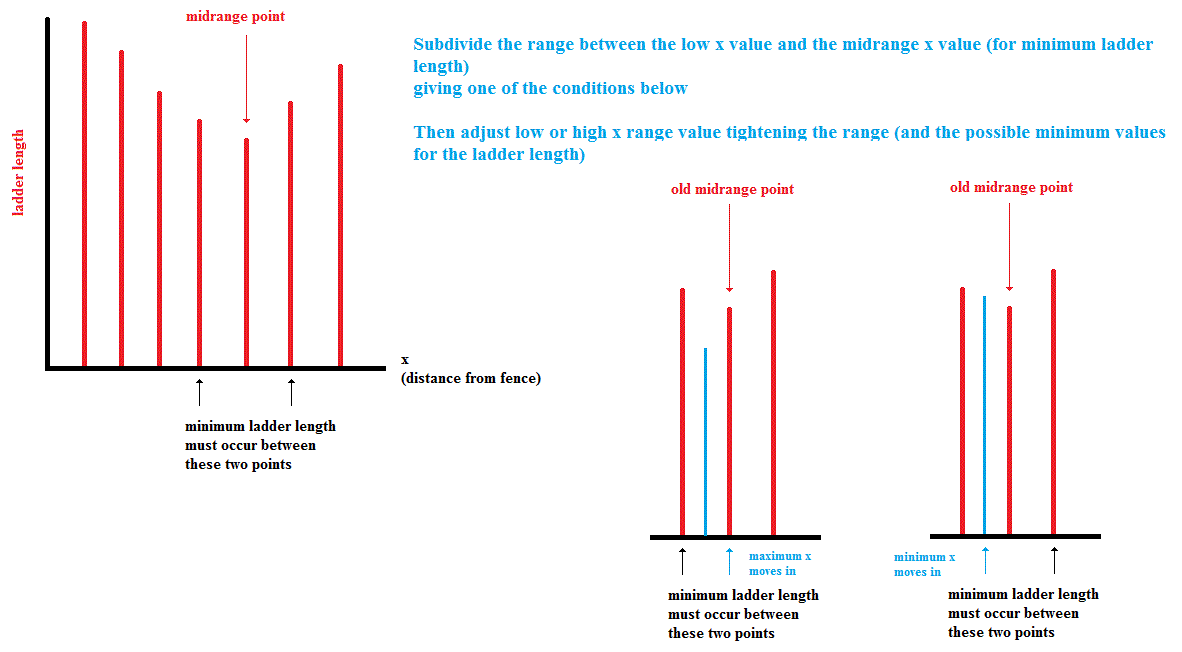
You could do perform this process by hand, but that's what computers were built for.

The implementation in a spreadsheet or simple programming language is straight forward.

Here is the result I got with a BASIC language program (5 minutes to write):

Minimum ladder length is between 10.800578 and 10.8005715
when the base of the ladder is between 1.8 and 1.80039063 feet away from the wall

If you can find somewhere to buy a ladder with a length more accurate than this, let me know!